

문제
이진 트리를 입력받아 전위 순회(preorder traversal), 중위 순회(inorder traversal), 후위 순회(postorder traversal)한 결과를 출력하는 프로그램을 작성하시오.

예를 들어 위와 같은 이진 트리가 입력되면,
- 전위 순회한 결과 : ABDCEFG // (루트) (왼쪽 자식) (오른쪽 자식)
- 중위 순회한 결과 : DBAECFG // (왼쪽 자식) (루트) (오른쪽 자식)
- 후위 순회한 결과 : DBEGFCA // (왼쪽 자식) (오른쪽 자식) (루트)
가 된다.
입력
첫째 줄에는 이진 트리의 노드의 개수 N(1 ≤ N ≤ 26)이 주어진다. 둘째 줄부터 N개의 줄에 걸쳐 각 노드와 그의 왼쪽 자식 노드, 오른쪽 자식 노드가 주어진다. 노드의 이름은 A부터 차례대로 알파벳 대문자로 매겨지며, 항상 A가 루트 노드가 된다. 자식 노드가 없는 경우에는 .으로 표현한다.
출력
첫째 줄에 전위 순회, 둘째 줄에 중위 순회, 셋째 줄에 후위 순회한 결과를 출력한다. 각 줄에 N개의 알파벳을 공백 없이 출력하면 된다.
문제 링크
1991번: 트리 순회
첫째 줄에는 이진 트리의 노드의 개수 N(1 ≤ N ≤ 26)이 주어진다. 둘째 줄부터 N개의 줄에 걸쳐 각 노드와 그의 왼쪽 자식 노드, 오른쪽 자식 노드가 주어진다. 노드의 이름은 A부터 차례대로 알파
www.acmicpc.net
풀이
문제 이름대로 트리를 순회하는 문제인데, 이 트리는 이진 트리다.
이진 트리라서 구현도 그리 어렵지 않게 할 수 있다.
그저 왼쪽과 오른쪽을 구분해주면서 값을 저장해주면 된다.
나는 어차피 자식 노드 값이 두 개 밖에 안들어오는데다가 왼쪽, 오른쪽 순서를 맞춰줘서 편하게 인덱스 0번은 왼쪽, 인덱스 1번은 오른쪽으로 구성했다.
트리 구현하는 방법은 여러가지이므로 원하는 방법을 참고하면 되니, 일단은 본론으로 들어가자.
전위 순회 동작
문제에 나와있는대로 (루트)(왼쪽 자식)(오른쪽 자식) 순서로 순회하는 방식을 전위 순회라고 한다.
예제 노드를 보면 이런 식으로 순회하게된다.▼

그러면 어떤 순서로 접근해야할까?
나는 아래의 순서대로 재귀함수를 짰다.
1. 일단은 정의대로 루트부터 시작을 한다.
다행히 루트는 A라고 알려줘서 루트를 찾는 과정은 생략해도 된다.
방문한 노드를 방문 순서 배열에 넣어준다.
방문 순서 배열에 넣어주나 바로 출력하나 같은 결과가 나올 것인데, swift특성상 여러 번 나눠서 출력하면 시간이 더 오래 걸릴것이기에 방문 순서 배열에 넣었다가 한 번에 연결해서 출력하기로 한 것이다.
`방문 순서 배열에 넣기 = 출력`
이라고 봐도 무방하다.▼

2. 왼쪽 노드와 오른쪽 노드가 둘 다 있다면, 왼쪽 노드를 먼저 들린 뒤 오른쪽 노드를 들린다.
dfs라서 맨 끝까지 탐색하게 되는데, 왼쪽을 우선으로 정해놔서 왼쪽 노드가 존재한다면, 계속 왼쪽으로 향하게 된다.
결국 오른쪽은 왼쪽을 다 탐색하고 나서 탐색이 시작된다.
재귀 함수를 두 번 실행시키는데, 첫번째 재귀 함수에는 B노드를, 두번째 재귀함수에는 C노드를 인수로 넣어준다.▼
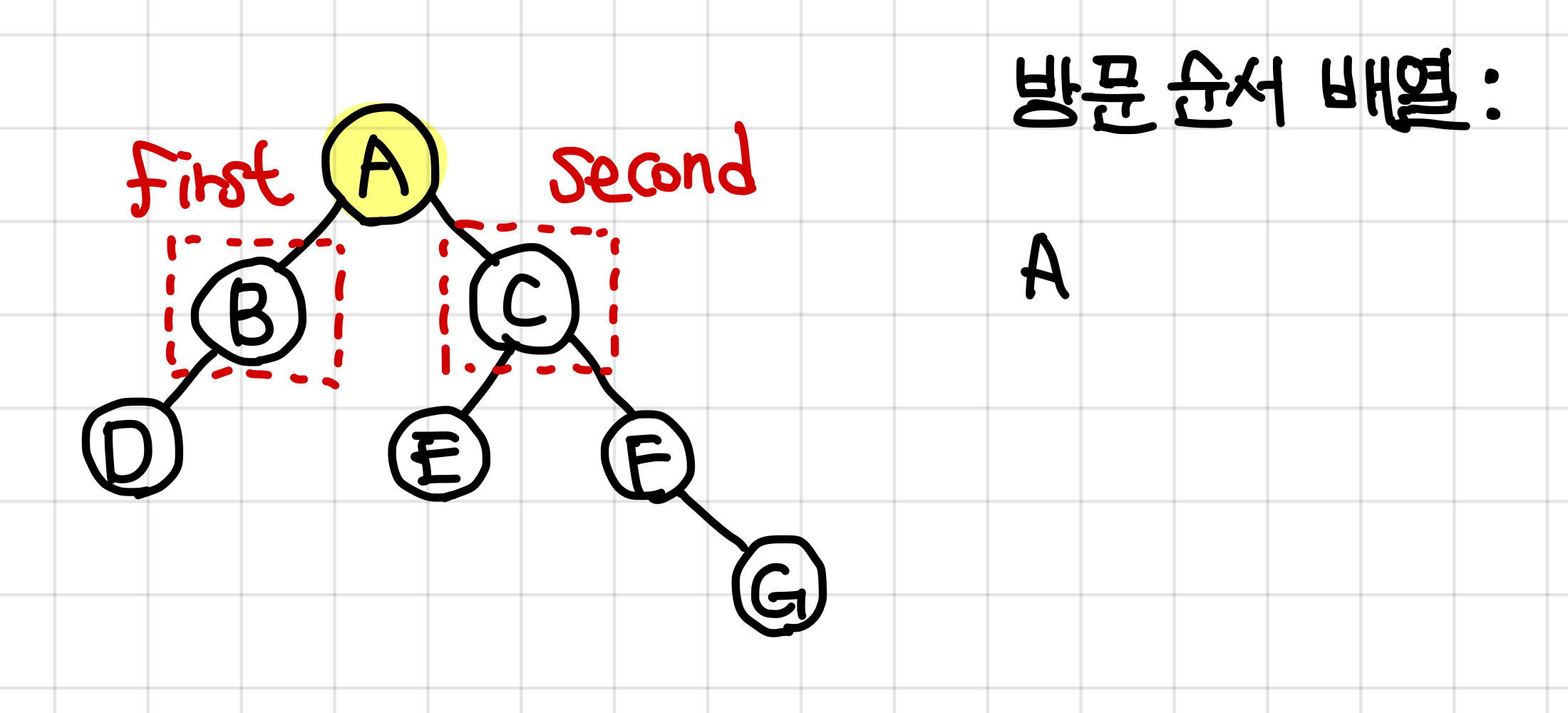
3. 왼쪽 노드인 B노드로 가기로 했으니까 B노드를 방문(탐색)하고, 방문한 B 노드를 방문 순서 배열에 넣어준다.
B 노드에는 오른쪽 노드가 없으므로 바로 다음 노드인 D노드로 가준다.
D노드를 재귀 함수의 인수로 넣어준다.▼

4. D노드로 가면 D 노드에는 자식 노드가 없으므로 더 이상 실행시킬 함수가 없어진다.
그러면 자연스럽게 왼쪽 dfs는 종료되고, 아까 넣어두었던 C노드로 재귀함수가 다시 실행된다.▼

5.A노드에서 했던 것과 동일하게 왼쪽을 우선으로 두 재귀함수를 실행시키면 된다.▼
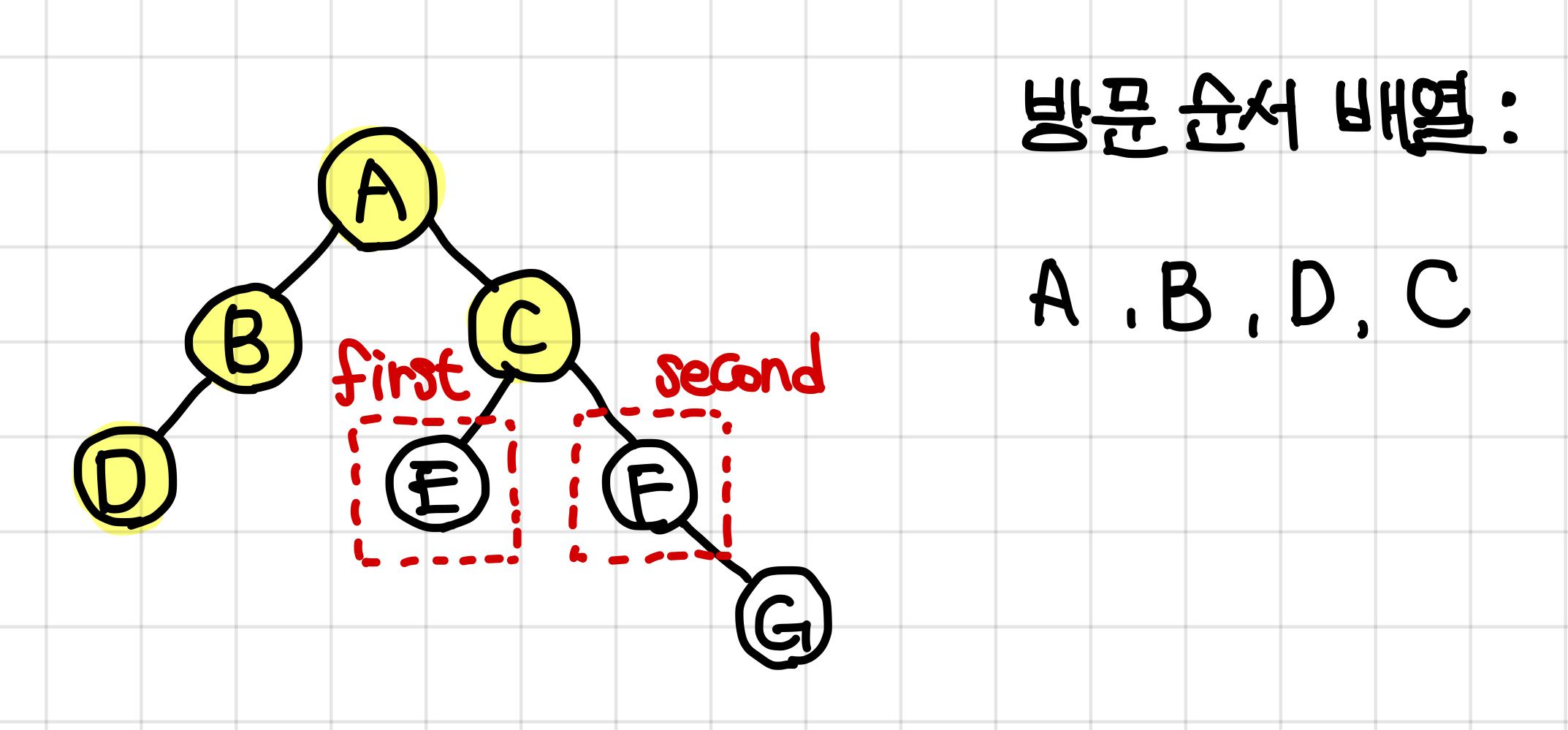
나머지 과정들은 똑같으므로 반복해주면 된다.
6. 결과는 이렇게 된다.▼
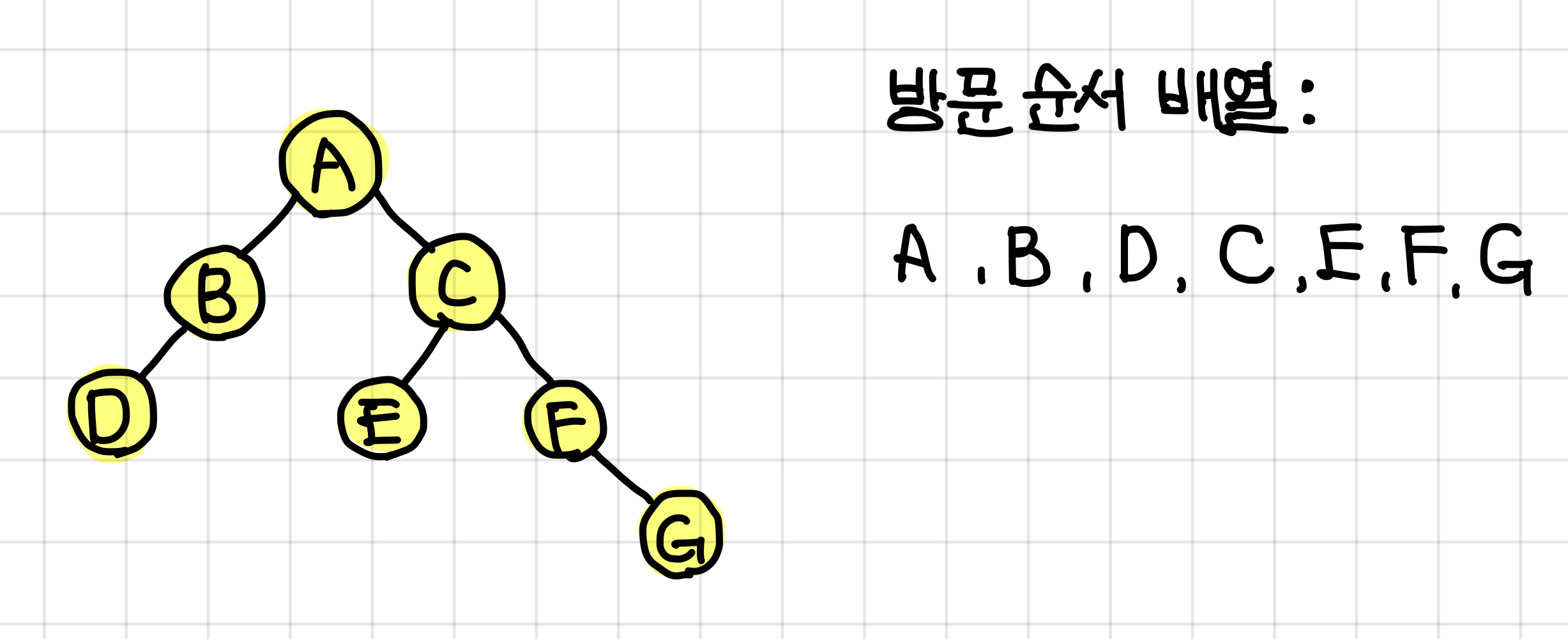
방문 순서 배열에 있는 원소들을 출력해주면 된다.
중위 순회 동작
문제에 나와있는대로 (왼쪽 자식)(루트)(오른쪽 자식) 순서로 순회하는 방식을 중위 순회라고 한다.
예제 노드를 보면 이런 식으로 순회하게 된다.▼
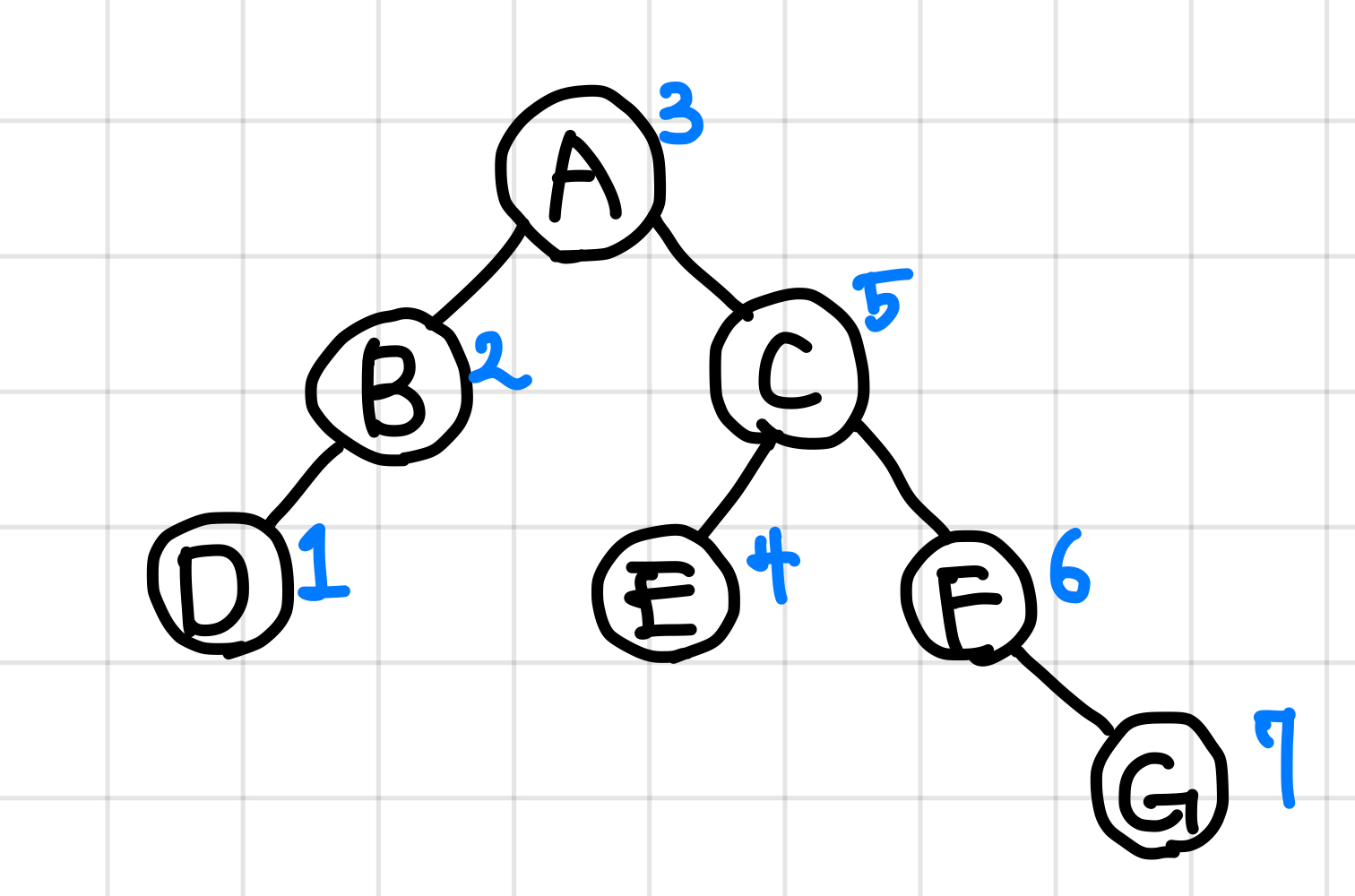
앞서 봤던 전위 순회의 경우에는 루트 노드부터, 맨 위부터 순회하라고 시작 값을 정해줬는데, 중위 순회는 순회를 시작할 값을 우리가 찾아야할 것 처럼 생겼다.
처음엔 그거 때문에 고민을 많이 했다.
'제일 아래 노드를 찾고 거슬러 올라와야 하나?'
그런데 생각해보니 우리는 자식 노드만 값으로 넣어줬지 부모 노드는 값으로 안넣어줬다.
거슬러 올라가게 하고 싶어도 올라가게 할 수 없다.
정보를 다시 저장해야하나 생각했는데, 그럴 필요가 없어졌다는 것을 알았다.
dfs에서 함수가 연달아 실행되는 것을 이용하기로 한 것이다.
1. 일단 시작은 루트 노드부터 한다.
하지만 전위 순회 처럼 방문 순서 배열에는 바로 넣지 않는다.
방문 순서 배열에 넣는 순서는 두 가지 경우로 나뉜다.
- 다음에 갈 노드가 왼쪽 노드
다음에 갈 노드가 왼쪽 노드라면 왼쪽으로 진행된 dfs함수가 다 끝나고 나서 값을 넣는다.
- 다음에 갈 노드가 오른쪽 노드
다음에 갈 노드가 오른쪽 노드라면 dfs함수가 실행되기 전에 값을 넣는다.
함수를 돌리고 값을 넣냐와 값을 넣고 함수를 돌리냐의 차이다.▼

하지만 뭐가 됐건 왼쪽부터 방문한다.
2. 왼쪽 부터 방문하기로 했으므로 A값은 왼쪽 dfs가 전부 끝나고 방문 순서 배열에 들어간다.
B값도 마찬가지다.
왼쪽 노드밖에 없어서 왼쪽으로 무조건 가야하기 때문에 앞에서 설명한 규칙대로 왼쪽 dfs가 끝나고 값을 넣는다.▼

3. 노드 D는 자식 노드가 없어서 실행 시킬 dfs가 없다.
따라서 D값을 방문 순서 배열에 넣어준다.▼
41
D로 인해 B에서 실행된 dfs가 끝이 났으므로 그 다음엔 B값이 들어간다.▼

B값이 들어갔다는 것은 A에서 실행된 dfs가 끝이 난 것이므로 A값도 들어간다.
그리고 앞서 C를 인수로 넣어둔 오른쪽 dfs가 실행된다.▼
7f
4. 노드 C의 경우에도 왼쪽과 오른쪽 노드가 전부 있으므로, 아까 루트 노드 A 처럼 왼쪽 dfs를 먼저 실행시키고 dfs가 끝나면 값 삽입, 그 다음에 오른쪽 dfs 실행 순서로 진행된다.▼

노드 E를 탐색한다.
5. 노드 E의 경우 아까의 D처럼 자식 노드가 없다.
따라서 왼쪽 dfs는 종료되고, E 값이 방문 순서 배열에 들어간다.▼
6c
그리고 C의 왼쪽 dfs도 종료된 것이므로 C값이 방문 순서 배열에 들어가고, F 노드를 탐색시작한다.▼
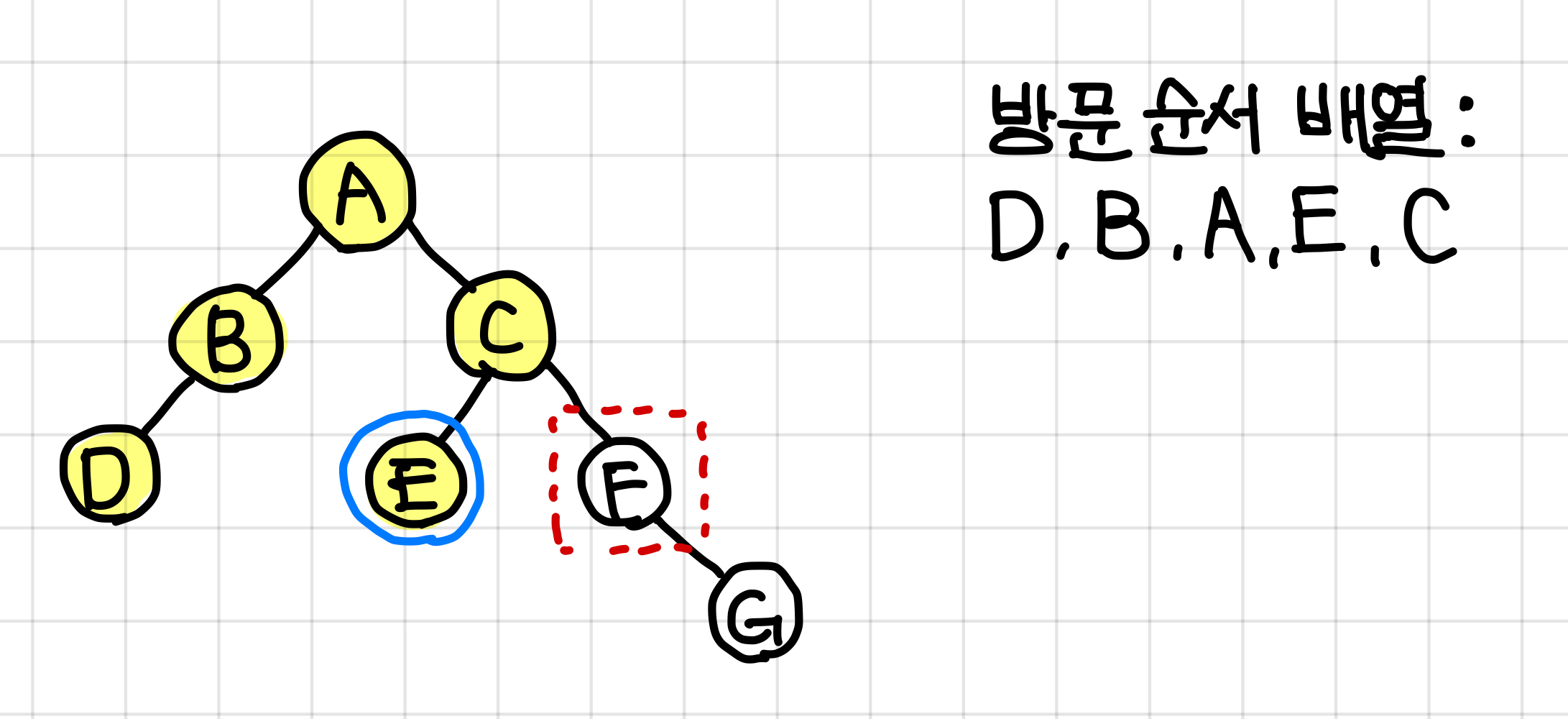
6. F 노드는 자식 노드가 G 하나뿐이지만, G 노드는 오른쪽 노드다.
따라서 F값을 먼저 방문 순서 배열에 넣고 dfs가 시작된다.▼

7. G 노드도 D와 E노드와 마찬가지로 자식 노드가 없으므로 방문 순서 배열에 값을 넣고 함수가 종료된다.▼

이제 방문 순서 배열을 출력하면 된다.
후위 순회 동작
문제에 나와있는대로 (왼쪽 자식)(오른쪽 자식)(루트) 순서로 순회하는 방식을 후위 순회라고 한다.
예제 노드를 보면 이런 식으로 순회를 한다.▼

후위 순회도 중위 순회에서 했던 고민처럼,
'하위 노드 구하는거부터 하고 거슬러 올라가야 하나?'
할 수 있지만, 사실 중위 순회랑 크게 다를게 없다.
중위 순회에서는 왼쪽 dfs 끝나면 값 넣고, 오른쪽 dfs가 실행되기 전에 값 넣고의 순서였다면,
후위 순회에서는 왼쪽 dfs 끝나고, 오른쪽 dfs 까지 다 끝나고 나서 값 넣기의 순서다.
그러면 자연스럽게 하위 노드부터 출력할 수 있게 된다.
물론 왼쪽 우선이다.
1. 루트 노드부터 시작을 한다.
왼쪽, 오른쪽 값이 둘 다 있다면 재귀 함수를 두 번 실행시키는데, 왼쪽 값이 인수로 들어간 재귀 함수를 먼저 실행시킨다.
A값은 왼쪽, 오른쪽 dfs가 모두 끝나면 넣는다.▼
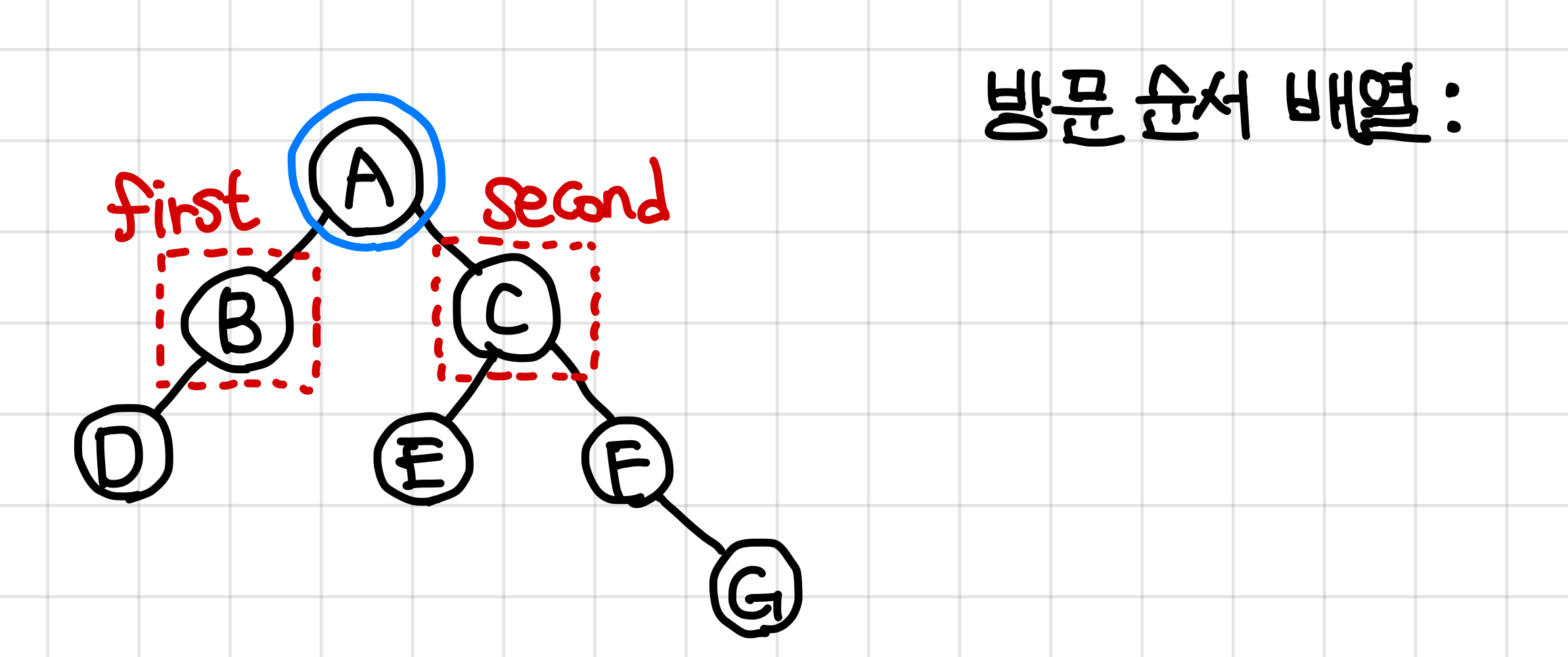
2. B노드도 1번 과정과 마찬가지로 자식 노드의 dfs를 모두 실행시키고 값을 넣는다.▼
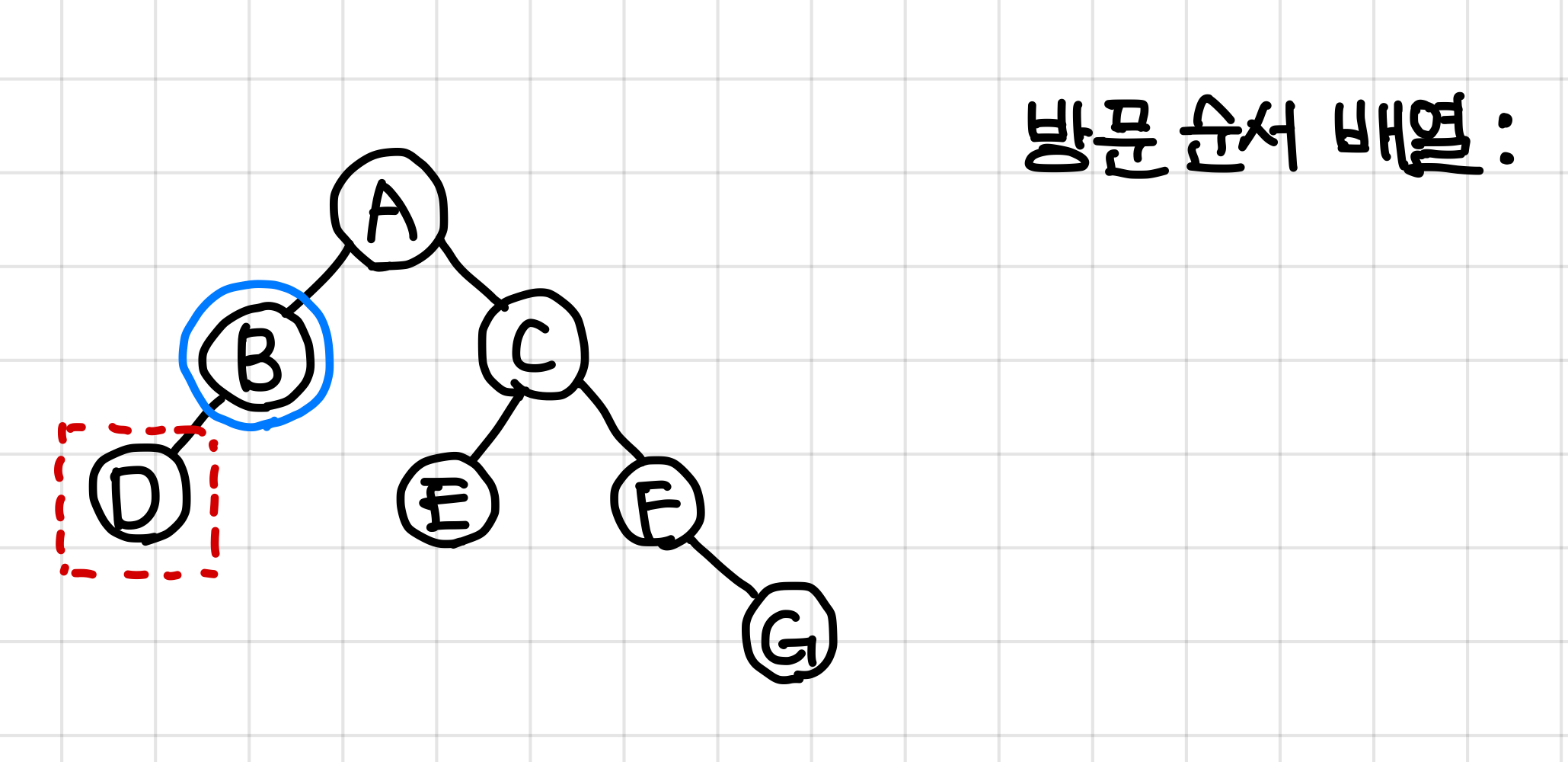
3. D노드는 자식 노드가 없다.
따라서 실행시킬 dfs함수가 없으므로 바로 값을 넣어준다.▼

값을 넣어줬다는 것은 B의 dfs함수가 전부 종료됐다는 것이므로, 다음엔 B값을 넣어준다.▼

A값은 아직 오른쪽 dfs가 종료되지 않았으므로 일단 C 노드 값으로 이동한다.▼

4. C 노드도 왼쪽, 오른쪽 노드 전부 존재하므로 두 dfs가 끝날 때 까지 값을 넣지 않는다.
일단은 E 노드로 이동한다.▼

5. E 노드는 D 노드와 마찬가지로 자식 노드가 없으므로 실행시킬 dfs함수가 없다.
그러므로 방문 순서 배열에 E값을 넣어준다.▼

E 값이 들어가서 왼쪽 dfs가 끝났지만 아직 C에게는 오른쪽 dfs가 남아있으므로 F로 넘어간다.
6. F 노드에겐 오른쪽 노드만 있으므로 오른쪽 dfs가 끝나고 값을 넣는다.▼

7. G 노드는 D와 E 노드처럼 자식 노드가 없으므로, G 값을 넣어준다.▼

G 값이 들어감과 함께 F 노드의 오른쪽 dfs가 종료됐으므로, F 값도 들어간다.▼
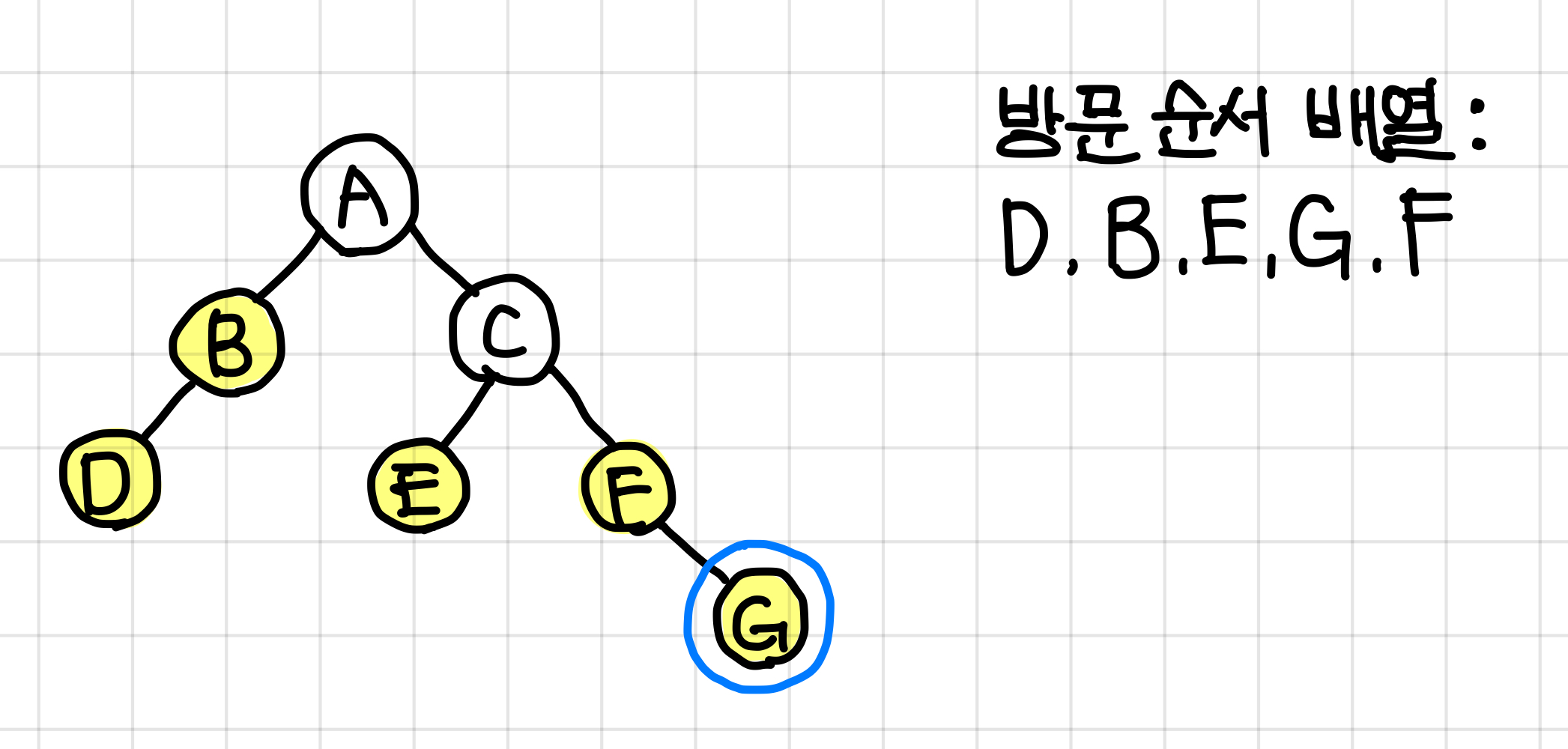
F 값이 들어가면서 C의 양쪽 dfs가 종료됐으므로 다음으론 C값이 들어간다.▼

마지막으로 C 값이 들어가면서 A의 양쪽 dfs가 종료됐으므로 A 값이 들어간다.▼

8. dfs가 전부 끝이 났으므로 출력해준다.
Swift 코드
let N = Int(readLine()!)!
var binaryTree = Array(repeating: [Int](), count: N + 1)
var visit = Array(repeating: false, count: N + 1)
var preOrderArr = [Character]()
var inOrderArr = [Character]()
var postOrderArr = [Character]()
for _ in 0..<N {
let input = readLine()!
var tmp = [Character]()
for i in input {
if i == " " {
continue
}
tmp.append(i)
}
binaryTree[Int(tmp[0].asciiValue! - 64)] = [tmp[1] == "." ? 0 : Int(tmp[1].asciiValue! - 64), tmp[2] == "." ? 0 : Int(tmp[2].asciiValue! - 64)]
}
func preOrderSearch(_ node: Int) {
visit[node] = true
preOrderArr.append(Character(UnicodeScalar(node + 64)!))
for i in 0..<2 {
if binaryTree[node][i] == 0 {
continue
}
if visit[binaryTree[node][i]] == true {
continue
}
preOrderSearch(binaryTree[node][i])
}
}
func inOrderSearch(_ node: Int) {
if binaryTree[node][0] != 0 && binaryTree[node][1] != 0 {
inOrderSearch(binaryTree[node][0])
inOrderArr.append(Character(UnicodeScalar(node + 64)!))
inOrderSearch(binaryTree[node][1])
} else if binaryTree[node][0] == 0 && binaryTree[node][1] != 0 {
inOrderArr.append(Character(UnicodeScalar(node + 64)!))
inOrderSearch(binaryTree[node][1])
} else if binaryTree[node][0] != 0 && binaryTree[node][1] == 0 {
inOrderSearch(binaryTree[node][0])
inOrderArr.append(Character(UnicodeScalar(node + 64)!))
} else {
inOrderArr.append(Character(UnicodeScalar(node + 64)!))
}
}
func postOrderSearch(_ node: Int) {
if binaryTree[node][0] != 0 && binaryTree[node][1] != 0 {
postOrderSearch(binaryTree[node][0])
postOrderSearch(binaryTree[node][1])
postOrderArr.append(Character(UnicodeScalar(node + 64)!))
} else if binaryTree[node][0] == 0 && binaryTree[node][1] != 0 {
postOrderSearch(binaryTree[node][1])
postOrderArr.append(Character(UnicodeScalar(node + 64)!))
} else if binaryTree[node][0] != 0 && binaryTree[node][1] == 0 {
postOrderSearch(binaryTree[node][0])
postOrderArr.append(Character(UnicodeScalar(node + 64)!))
} else {
postOrderArr.append(Character(UnicodeScalar(node + 64)!))
}
}
preOrderSearch(1)
inOrderSearch(1)
postOrderSearch(1)
print(preOrderArr.map { String($0) }.joined(separator: ""))
print(inOrderArr.map { String($0) }.joined(separator: ""))
print(postOrderArr.map { String($0) }.joined(separator: ""))
`Substring`과 `String`을 `Character`로 형변환하느라 엄청나게 오래걸렸다...
`String`이 왜 `Character`로 안 바뀌는 건가 조금 유추를 해봤는데, 아무래도 `String`은 글자가 하나가 아닌 경우가 더 많아서 인거 같다.
상식적으로 다시 생각해보니 여러개의 문자를 한 개의 문자로 형변환하는게 말이 안되긴 하다.
그거랑 인덱스 번호를 노드로 설정하려고 A를 아스키 코드 값으로 변환해서 64를 빼주느라 개고생했다.
최근들어 다시 생각해보니, Swift의 `String`은 아스키코드가 아닌 유니코드라서 형변환이 안되는 거 같다.
C++ 코드
#include <iostream>
using namespace std;
int n;
int tree[26][2];
void preorder(int x) {
if (x < 0)
return ;
cout << (char)(x + 65);
preorder(tree[x][0]);
preorder(tree[x][1]);
}
void inorder(int x) {
if (x < 0)
return ;
inorder(tree[x][0]);
cout << (char)(x + 65);
inorder(tree[x][1]);
}
void postorder(int x) {
if (x < 0)
return ;
postorder(tree[x][0]);
postorder(tree[x][1]);
cout << (char)(x + 65);
}
void input() {
char a, b, c;
cin >> n;
for (int i = 0; i < n; i++) {
cin >> a >> b >> c;
tree[a - 65][0] = b - 65;
tree[a - 65][1] = c - 65;
}
}
void solution() {
preorder(0);
cout << '\n';
inorder(0);
cout << '\n';
postorder(0);
cout << '\n';
}
void solve() {
input();
solution();
}
int main() {
solve();
}
입력을 숫자가 아닌 문자로 받아서 약간 곤란했다.
트리 정보를 주는 문제면 어차피 서로 다른 값들을 줄 것이기도 하고, 서로 다른 값이니까 받아온 값을 인덱스로 사용하기도 좋다.
근데 문자로 들어와서 받아온 값을 인덱스로 사용할 수가 없어서, 벡터로 받은 다음에 인덱스를 다른 변수로 쓸까 고민했다.
변수 하나 추가되는 것이긴 한데 깔끔하지 않을거 같아서 그냥 문자를 정수화 시켜버린 뒤에 그 값을 인덱스로 사용했다.
함수 작동은 잘 보면 알겠지만, 출력과 재귀가 어떻게 돌아가냐의 차이라서 굉장히 쉽고 간결하게 구현할 수 있다.
Swift로 풀었을 때는 형변환이 정말..(심한 말) 같았는데, C++로 하니까 정말 쾌적하다…
'Algorithm > PS' 카테고리의 다른 글
| 백준 2346번 풍선 터뜨리기 - SWIFT (0) | 2024.05.13 |
|---|---|
| 백준 2193번 이친수 - SWIFT (0) | 2024.05.13 |
| 백준 1992번 쿼드트리 - SWIFT (0) | 2024.04.28 |
| 백준 1987번 알파벳 - SWIFT (0) | 2024.04.19 |
| 백준 1967번 트리의 지름 - SWIFT (0) | 2024.04.18 |




