

문제
0과 1로만 이루어진 수를 이진수라 한다. 이러한 이진수 중 특별한 성질을 갖는 것들이 있는데, 이들을 이친수(pinary number)라 한다. 이친수는 다음의 성질을 만족한다.
- 이친수는 0으로 시작하지 않는다.
- 이친수에서는 1이 두 번 연속으로 나타나지 않는다. 즉, 11을 부분 문자열로 갖지 않는다.
예를 들면 1, 10, 100, 101, 1000, 1001 등이 이친수가 된다. 하지만 0010101이나 101101은 각각 1, 2번 규칙에 위배되므로 이친수가 아니다.
N(1 ≤ N ≤ 90)이 주어졌을 때, N자리 이친수의 개수를 구하는 프로그램을 작성하시오.
입력
첫째 줄에 N이 주어진다.
출력
첫째 줄에 N자리 이친수의 개수를 출력한다.
문제 링크
https://www.acmicpc.net/problem/2193
풀이
이친수 옆에 친절하게 pinary number라고 영어로 써놨길래 실제로 많이 쓰이는 건가 싶어서 영어로 검색해보니 딱히 나오는게 없었다...
뭔가 속은 기분이 들었지만, 규칙이 간단해서 쉽게 풀 수 있는 문제였다.
아래는 이친수의 규칙이다.
- 이친수는 0으로 시작하지 않는다.
- 이친수에서는 1이 두 번 연속으로 나타나지 않는다. 즉, 11을 부분 문자열로 갖지 않는다.
맨 앞이 1이 아니면서, 1이 연속하지 않는 수의 개수를 구하면 되는 것이었다.
그래서 필자는 DP테이블을 아래와 같이 설정했다.
0번째 행의 의미는 맨 끝에 0이 붙었을 때, 1번째 행의 의미는 맨 끝에 1이 붙었을 때를 의미한다.▼

우선 위의 이친수의 규칙을 생각해보기 전에 이진수를 이렇게 생각을 해볼 수 있다.
N - 1자리 이진수들 뒤에 0 또는 1을 붙여주면 N자리 이진수를 만들 수 있다.
이와 똑같이, N - 1자리 이친수들 뒤에 0 또는 1을 붙여주면 N자리 이친수를 만들 수 있다.▼

하지만 이친수의 경우, 0은 아무 이친수 뒤에 붙을 수 있지만 1은 1로 끝나는 이친수 뒤에 붙을 수 없다.▼

그래서 간단하게 이친수의 개수 규칙을 구하면 아래와 같다.
- N자리 이친수 맨 뒤에 1이 붙을 수 있는 경우: 맨 뒤에 0이 붙은 N - 1자리 이친수
- N자리 이친수 맨 뒤에 0이 붙을 수 있는 경우: N - 1 자리 이친수
이를 DP 테이블로 다시 보면 이렇게 된다.▼
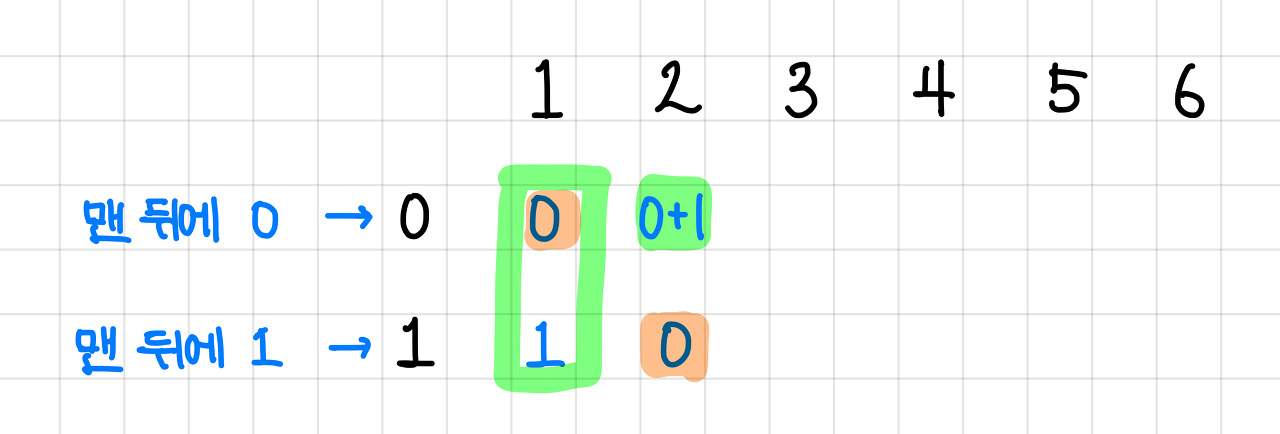
그래서 이 규칙대로 DP 테이블을 채워주면 아래와 같이 된다.▼
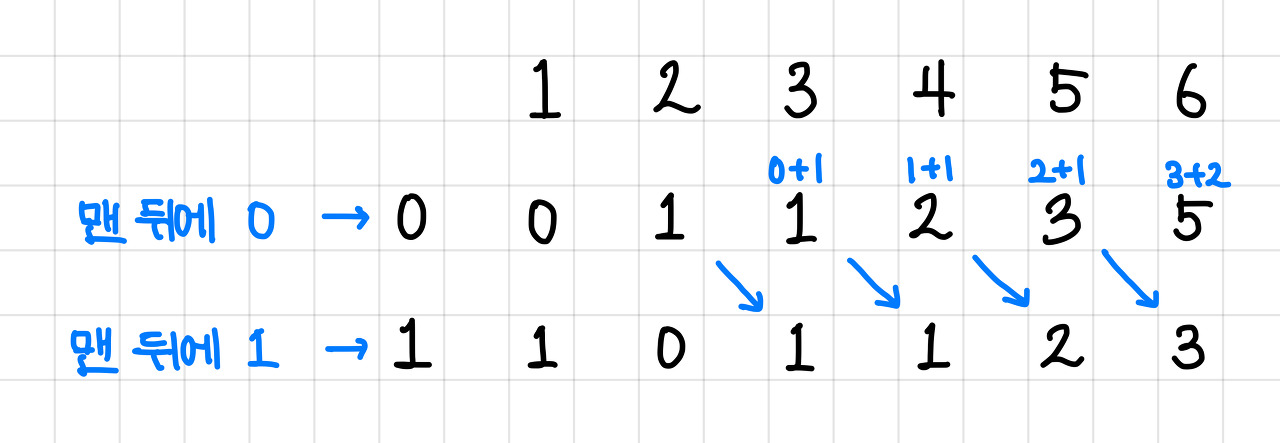
위의 규칙대로 DP 테이블을 계속 채워주면 된다.
프로그램 동작
위의 풀이에 나온 규칙대로 각 행들을 차례대로 채워주고 마지막의 열의 값들을 모두 더해 출력했다.
간단하게 구현할 수 있다.
Swift 코드
let N = Int(readLine()!)!
var A = Array(repeating: Array(repeating: 0, count: 2), count: 91)
A[1][0] = 0
A[1][1] = 1
A[2][0] = 1
A[2][1] = 0
if N > 2 {
for i in 3...N {
A[i][0] = A[i - 1][0] + A[i - 1][1]
A[i][1] = A[i - 1][0]
}
}
print(A[N][0] + A[N][1])
'Algorithm > PS' 카테고리의 다른 글
| 백준 2407번 조합 - SWIFT (0) | 2024.05.13 |
|---|---|
| 백준 2346번 풍선 터뜨리기 - SWIFT (0) | 2024.05.13 |
| 백준 1991번 트리 순회 - SWIFT, C++ (0) | 2024.04.28 |
| 백준 1992번 쿼드트리 - SWIFT (0) | 2024.04.28 |
| 백준 1987번 알파벳 - SWIFT (0) | 2024.04.19 |




