개론
전에 배운 B트리는 구조 변경이 자주 일어난다는 점에서 한계가 보였다.
조회는 빠른 편이지만, 삽입과 삭제와 같이 DB에 변경이 자주 일어나게 되면 연산량이 많아진다는 단점이 있었다.
그래서 이를 보완하고자 나온 것이 B+트리이다.
특징
B 트리와 다른 점.
- 모든 데이터가 리프노드에 모여있다.
- 모든 리프노드는 연결리스트 형태를 띄고 있다.
- 리프노드의 부모 key는 리프노드의 첫번째 key보다 작거나 같다.
B트리와 같은 점.
- 노드에는 최대 $M-1$개 부터 $\lceil \frac{M}{2} \rceil - 1$개의 데이터가 포함된다.
- 특정 노드의 데이터(key)가 $K$개라면, 자식 노드의 개수는 $K+1$개여야 한다.
- 특정 노드의 왼쪽 서브 트리는 특정 노드의 데이터보다 작은 값, 오른쪽 서브 트리는 큰 값으로 구성된다.
- 내부 노드(루트노드와 리프노드 제외 노드들)는 최소$\lceil \frac{M}{2} \rceil$, 최대 $M$개의 자식을 가질 수 있다. 최대 $M$개의 자식을 갖는 B 트리를 $M$차 B 트리라고 한다.
조회
조회는 이진 탐색과 유사하게 진행된다.
찾고 싶은 값을 14라고 해보자.▼
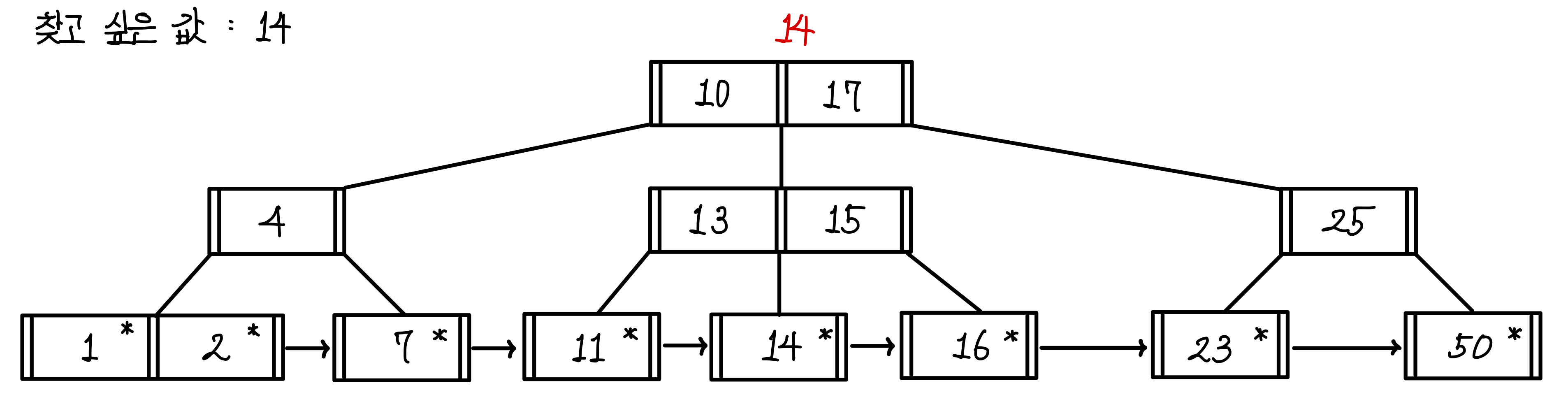
조회는 하향식으로 이루어진다.
루트 노드에서부터 값의 범위를 확인한다.
14는 10과 17 사이의 값이기 때문에 가운데 경로로 내려간다.▼
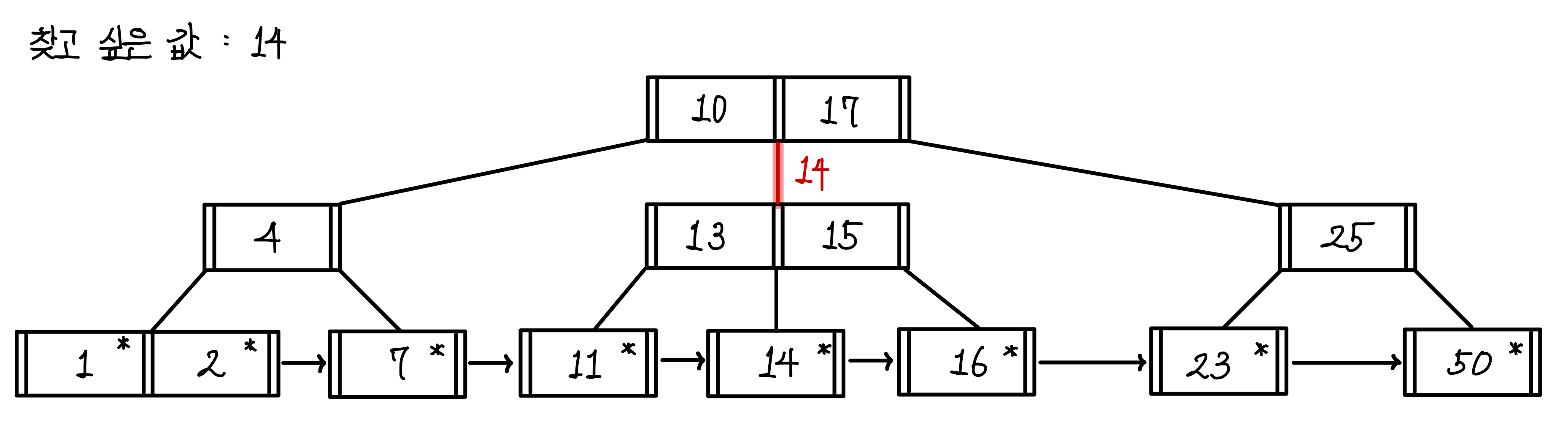
내부 노드로 내려와서도 똑같은 방법으로 탐색한다.
14는 13과 15 사이의 값이므로 이번에도 가운데 경로로 내려간다.▼

가운데 경로로 내려가서 값을 탐색했을 때 14가 있으므로 조회에 성공한다.▼
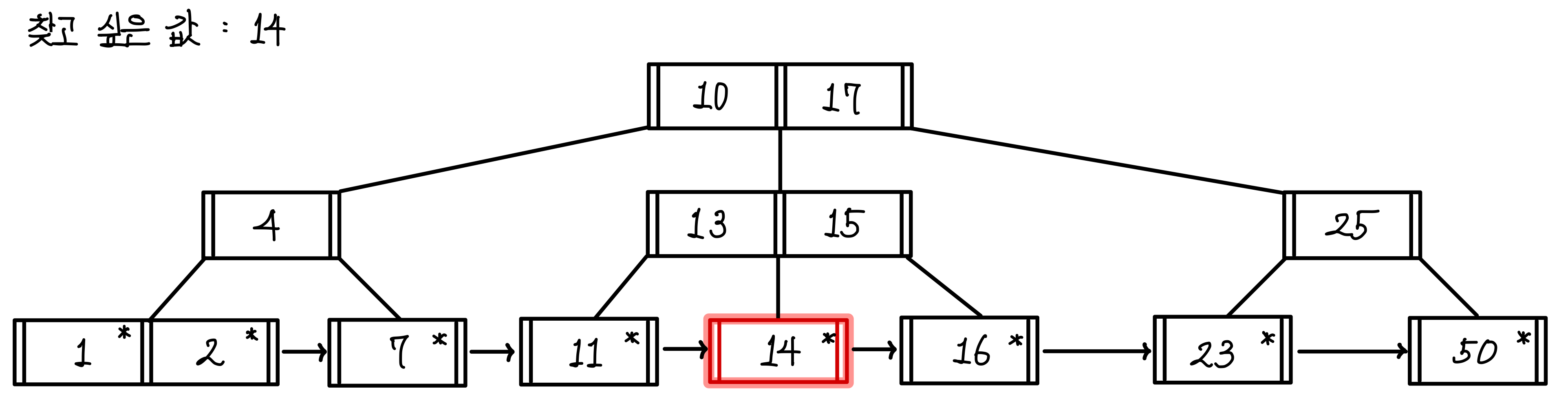
이진탐색의 기법을 유사하게 따라가기 때문에 값의 범위에 맞지 않는 트리는 모두 무시할 수 있다.
이런 식으로 빠른 속도로 값을 조회할 수 있다.
삽입
1, 3, 5, 19, 12의 값을 순서대로 3차 B+ Tree에 삽입하는 것을 예제로 보자.
1 삽입
1을 삽입하면, 루트 노드이자 리프 노드로 들어가게 된다.▼
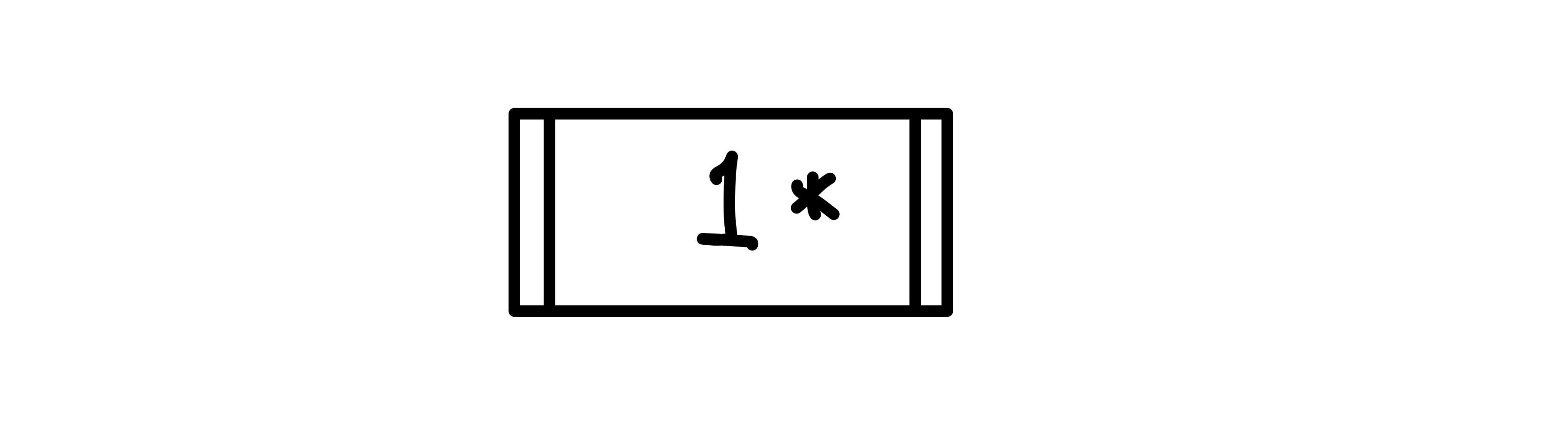
3 삽입
3을 삽입하면 1의 오른쪽에 붙게 된다.
아직까지는 분할이 일어나지 않는다.▼
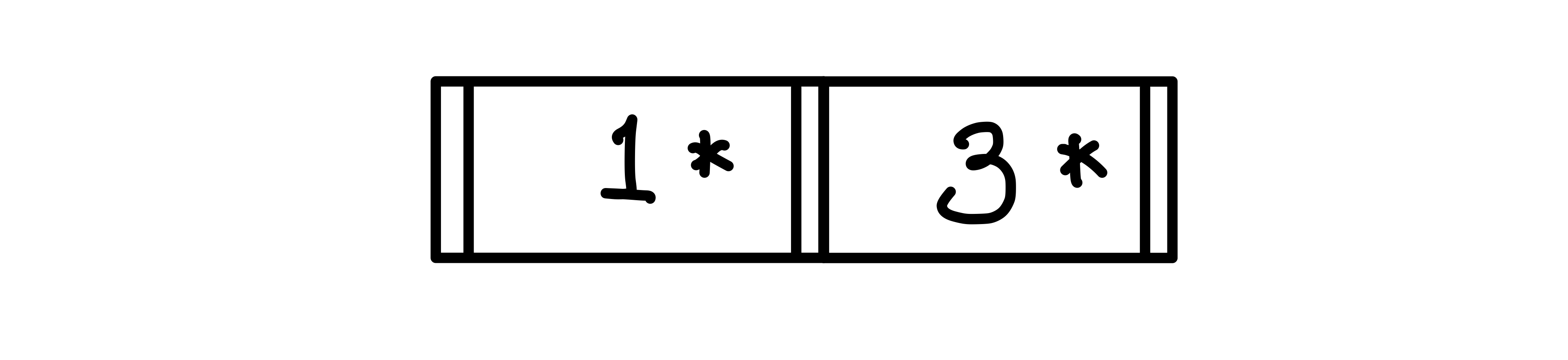
5 삽입
5를 삽입하면 3의 오른쪽에 붙게 된다.
하지만 3차 B+ Tree의 한 노드는 2개의 값만 가질 수 있기에 포화상태가 된다.
포화 상태가 되면 노드에 있는 값들 중, 가운데 값을 복제해 인덱스로 사용한다.
그리고 인덱스를 기준으로 값을 분할하고 인덱스의 포인터로 이어준다.▼
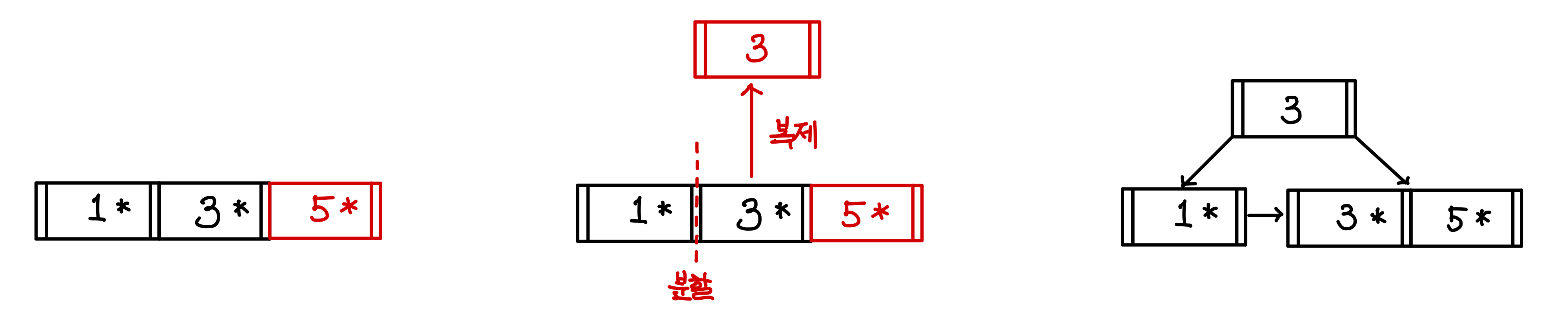
19 삽입
19를 삽입하면 5의 오른쪽에 붙게 된다.
이번에도 포화상태가 되기 때문에 3, 5, 19가 있는 노드의 중간 값인 5를 복제하여 인덱스로 만들어 3 옆에 붙여준다.▼

12 삽입
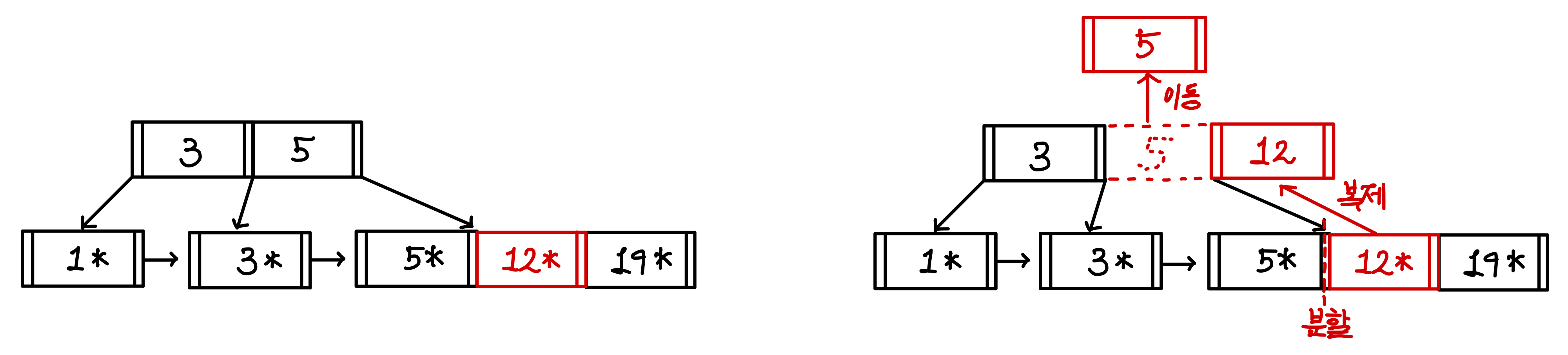
12를 삽입하게 되면 5와 19 가운데에 들어가게 된다.
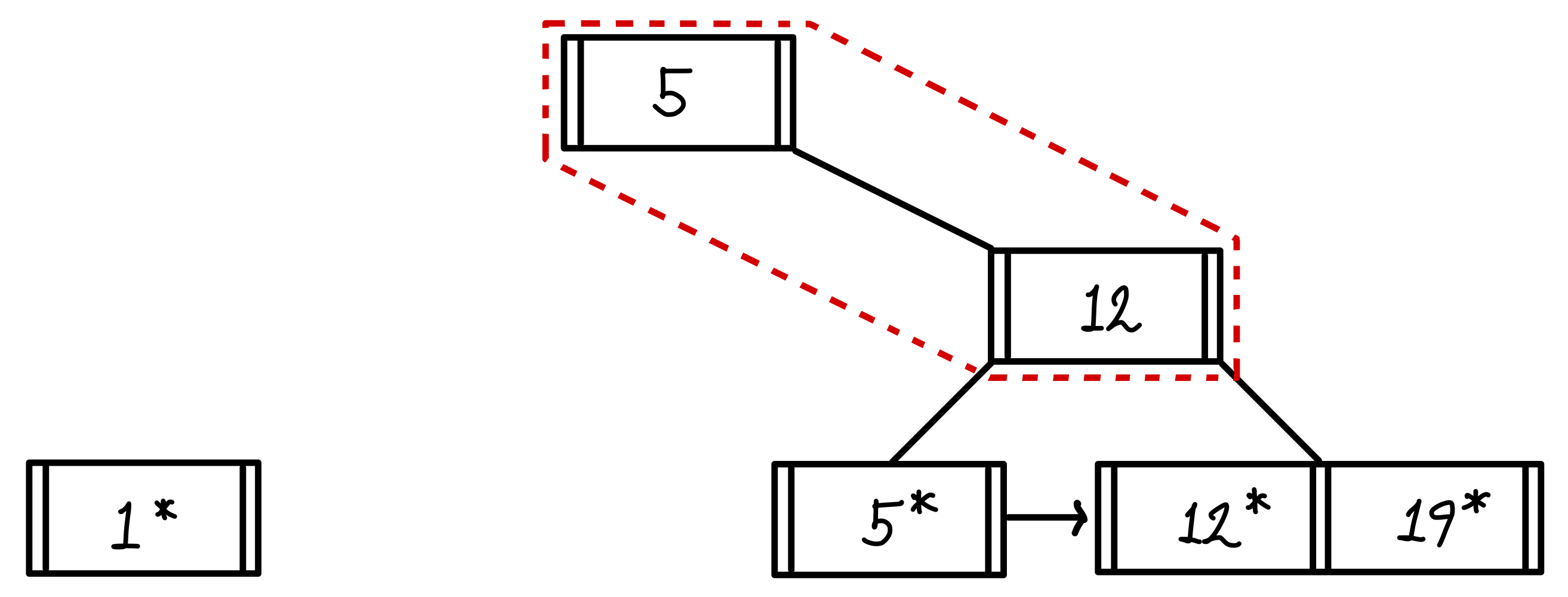
이번에도 포화상태가 되기 때문에 5, 12, 19가 있는 노드의 중간 값인 12를 복제하여 인덱스로 만들어 5 옆에 붙여준다.
이러면 인덱스도 포화상태가 되어 다시 3, 5, 12에서 다시 중간 값을 고른다.
하지만 이번에는 리프노드와는 다르게 복제하지 않는다.
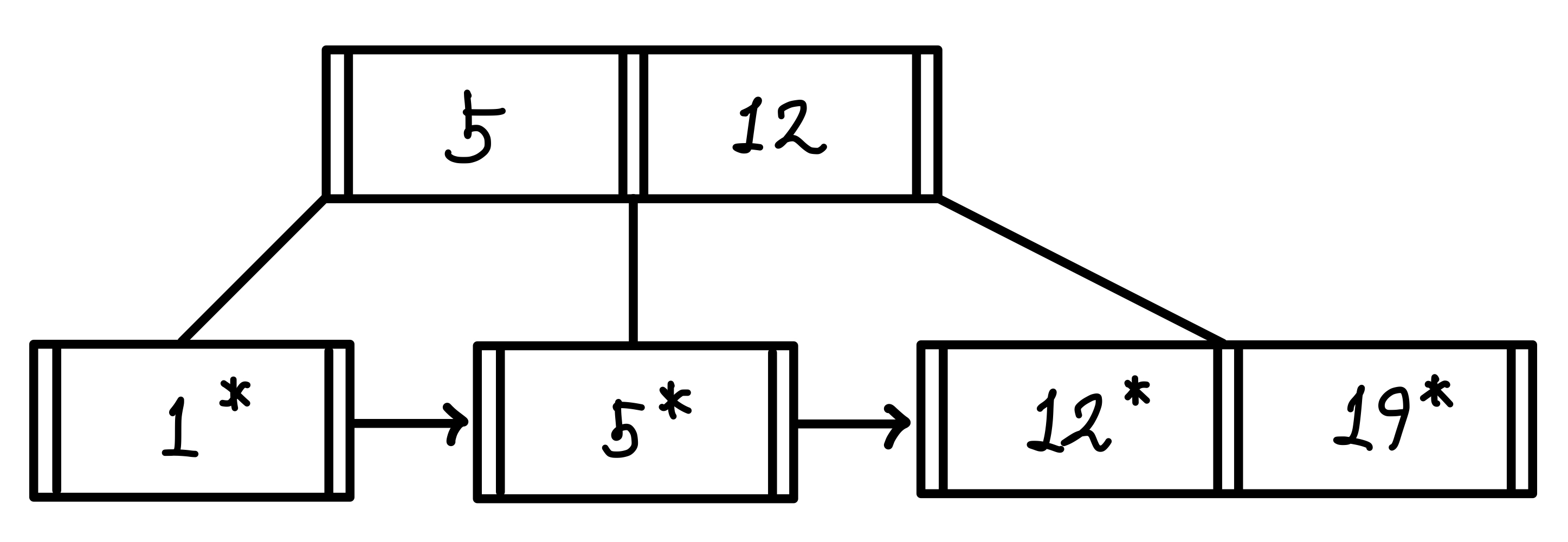
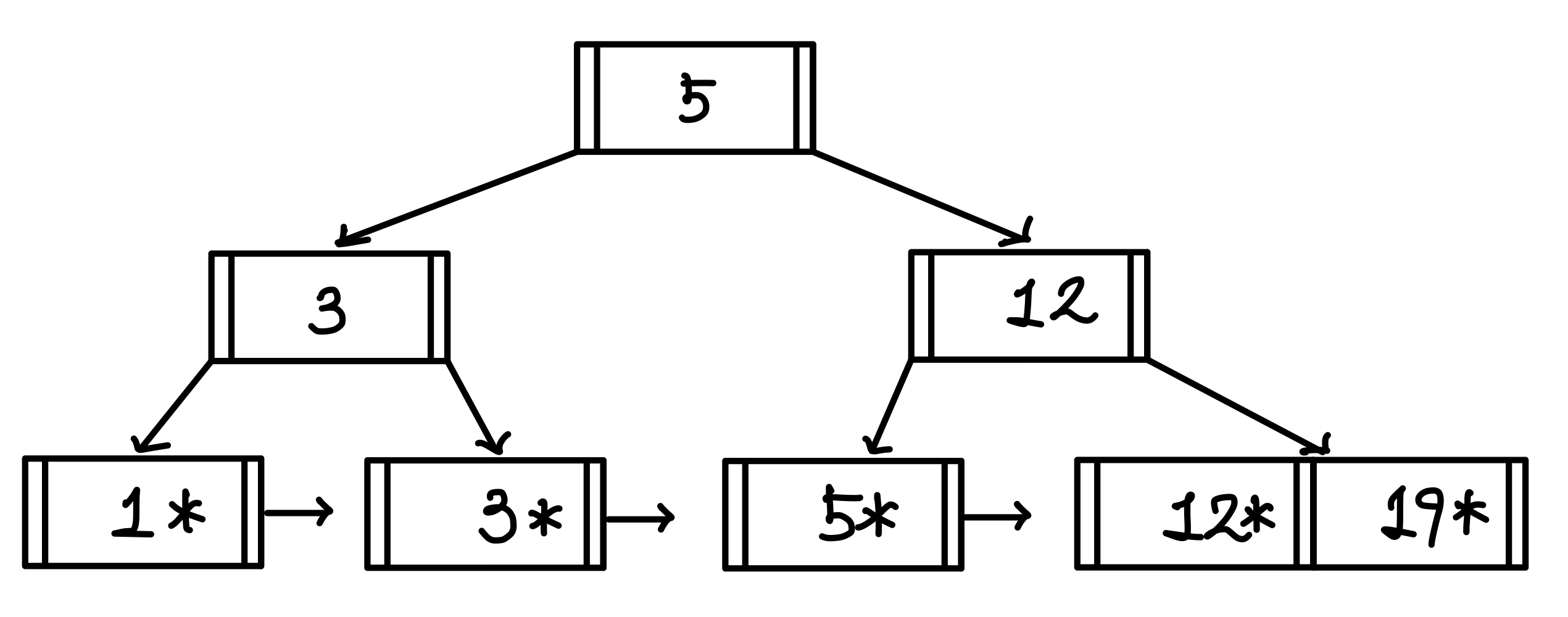
중간 값으로 선택된 5가 복제되는 것이 아닌, 값 자체가 윗 계층으로 올라간다.▼
삭제
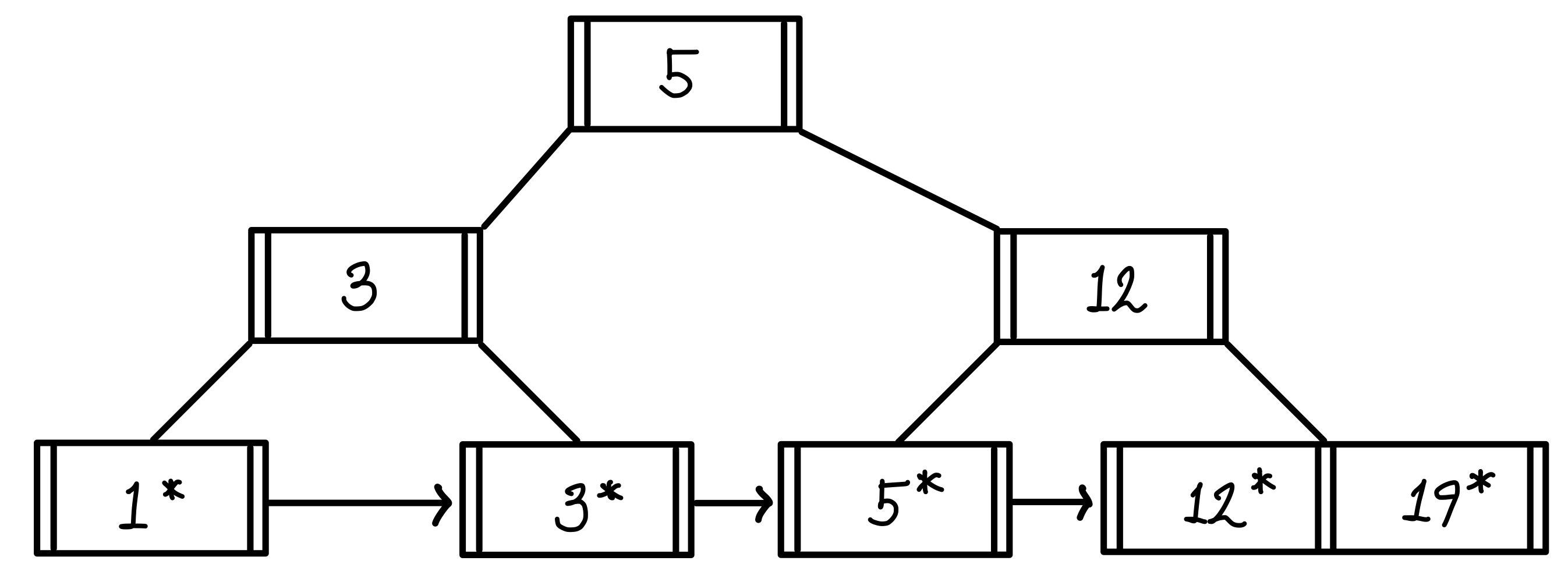
위의 예제에서 삭제하는 경우를 보자.
키 조건을 만족하는 삭제
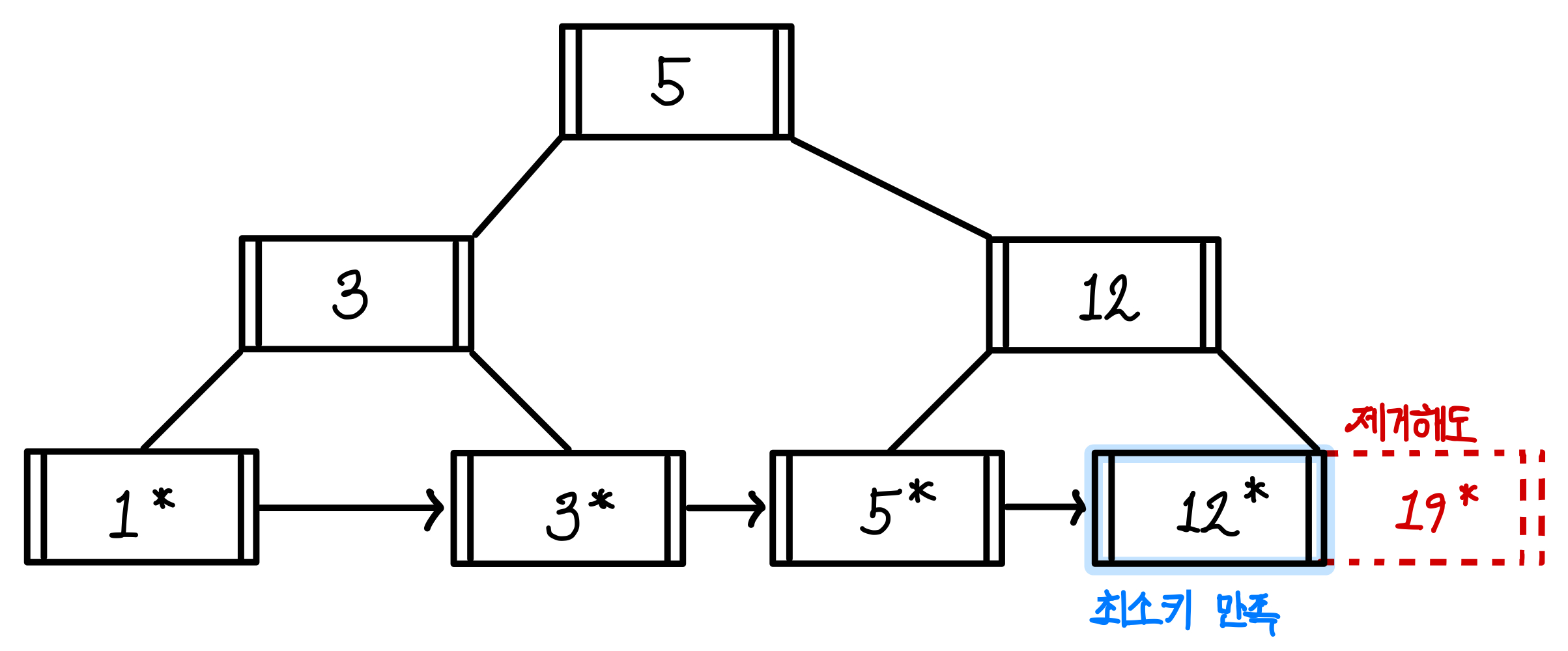
위의 예제에서 19를 삭제한다고 해보자.
이 경우 최소키를 만족하기에 단순히 조회하고 제거만 해주면 된다. ▼
키 조건을 만족하지 않는 삭제
이번에는 3을 삭제한다고 해보자.
3을 삭제하면 최소키 조건을 만족하지 않아 인덱스를 수정해야한다. ▼

인덱스를 타고 올라갔을 때, 제거한 3과 같기에 인덱스도 같이 제거된다. ▼
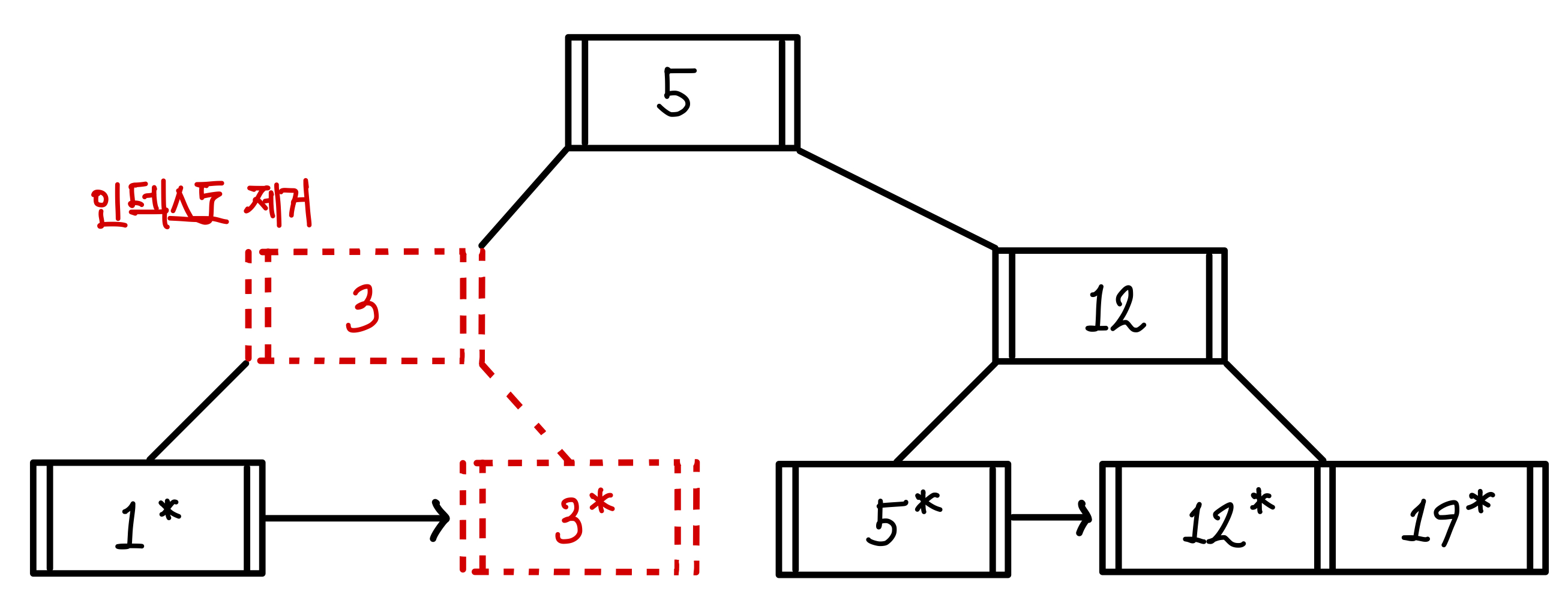
인덱스도 제거되면서 재조정이 되어 부모 노드인 5와 12로 재조정이 된다. ▼