

개론
"인덱싱(indexing)이란 무엇일까?"
뉴스 기사를 수집한다고 해보자.▼

수집한 뉴스 기사를 조회한다고 할 때, 수집한 뉴스 기사의 개수가 많으면 원하는 기사를 찾는게 쉽지 않을 것이다.▼

그런데 뉴스 기사를 기사 주제에 따라 쪽수로 표시하면 찾기가 훨씬 쉬워질 것이다.
곰 주제는 266쪽 부터 369쪽, 고라니 주제는 370쪽부터 500쪽 등등…▼

그런데 이렇게 크게 나눠버리면 찾기 쉬워진 것은 맞으나 세부적인 기사를 찾기가 힘들다.
예를 들어 곰 주제에서 ‘곰돌이 푸가 성공한 이유’라는 주제를 찾으려면 266쪽으로 가서 369쪽까지 쭉 훑어봐야한다.▼

그렇기에 대분류로 한 번 나누고 다시 소분류로 ‘곰돌이 푸가 성공한 이유’라는 뉴스 기사를 다시 한 번 쪽수를 분류 해야한다.▼
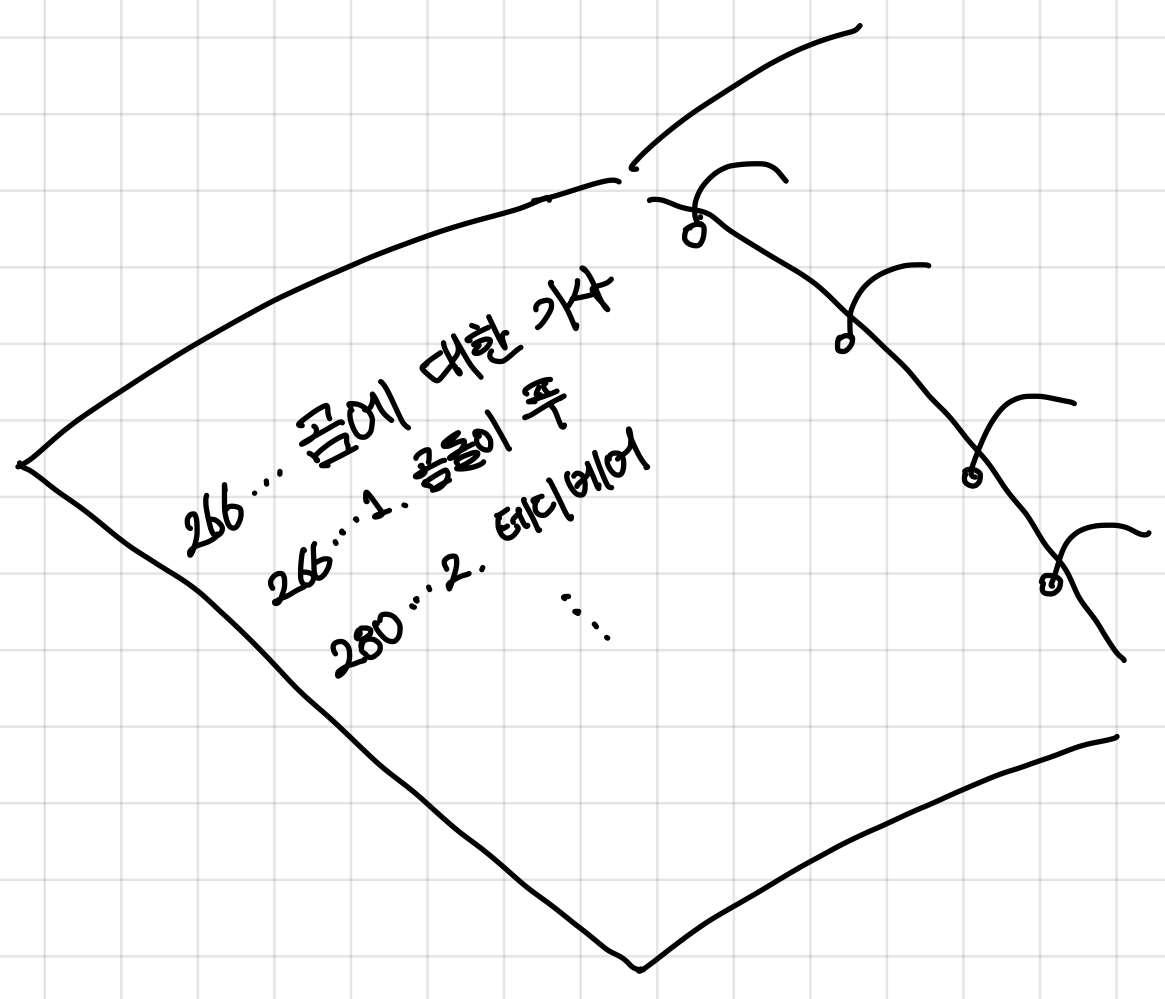
이런 과정을 거치고 나면 ‘곰돌이 푸가 성공한 이유’ 이라는 기사는 266쪽에 있다고 알 수 있을 것이고, 더 이상 하나하나 찾아보지 않고 한 번에 어디 있는지 알게 된다.

이렇게 원하는 데이터가 어디있는지 표시를 하고 쉽게 찾게 해주는게 인덱싱이다.
한 번에 찾아갈 수 있게 포스트잇이나 책갈피를 껴놓는 것과 같다.
인덱싱의 기본적인 요소들
Heap
자료구조에서 봐서 익숙하다는 생각이 들 수 있지만, 이 heap은 단순히 더미라는 의미이다.
우선순위큐와 같이 정렬이 되는 그런 구조가 아니다.
구조/삽입
힙은 아래의 그림과 같이 들어온 순서대로 쌓아준다.▼
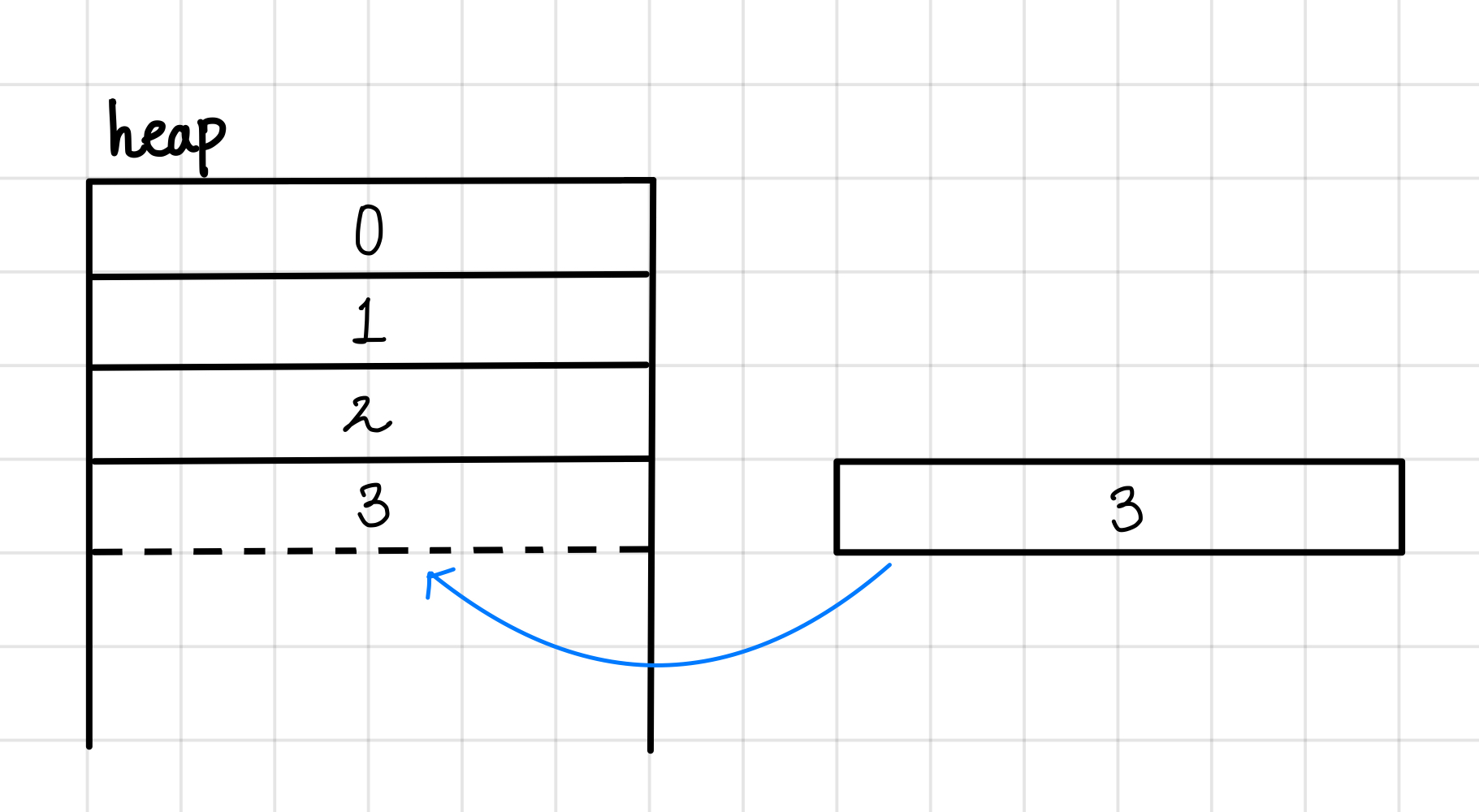
힙은 들어온 순서대로 쌓으면 되는 구조이므로 단순 저장하는데 적합하다.
조회
그렇다면 조회는 어떤 식으로 이뤄질까?
뭔가 특별한 방법이라도 있는걸까?
아쉽게도 힙에는 그런 특별한 방법은 없다.
전체 데이터를 쭉 순회하는 전수 조사방식으로 조회를 한다.▼

삭제
뭔가를 지울 때도 전수 조사를 통해 레코드를 찾는다.
우선 적절히 순회하여 중간에 있던 레코드를 지웠다고 해보자.▼
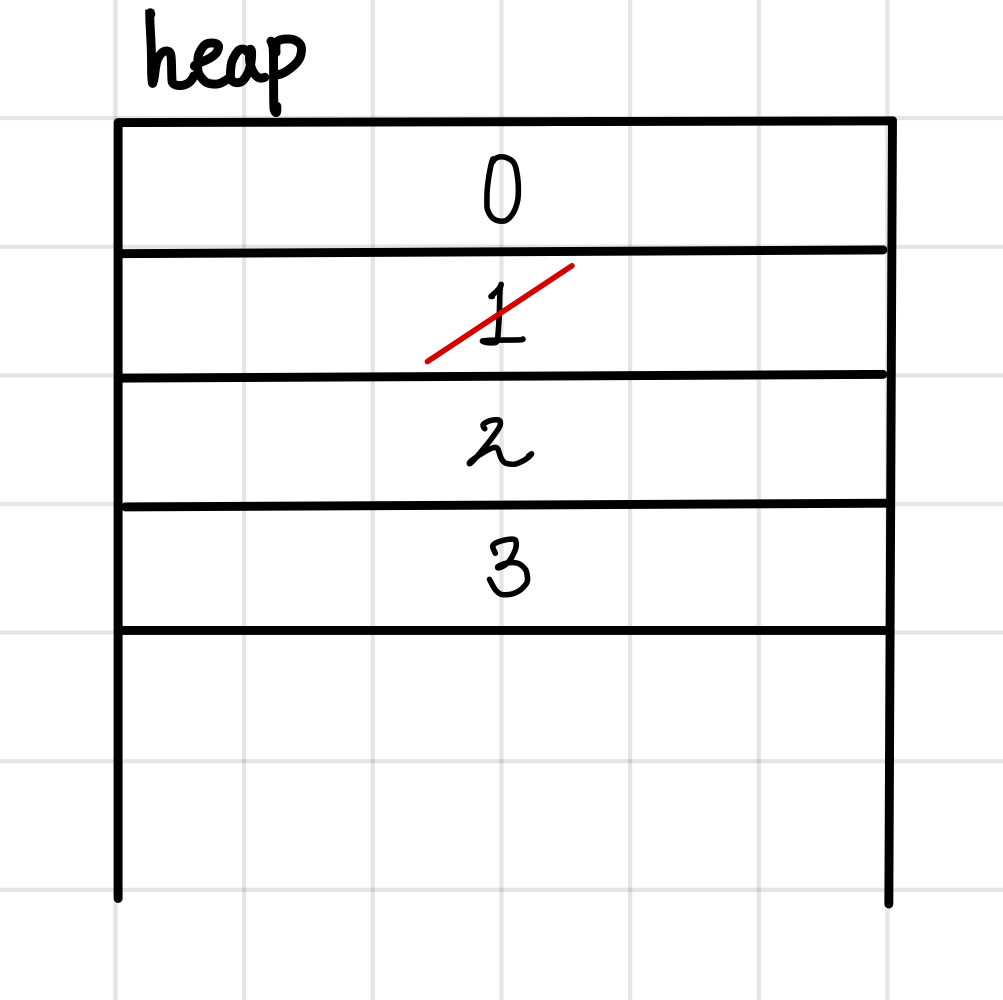
그렇다면 새로운 레코드가 추가 되면 빈 공간에 들어갈까?
아쉽게도 힙에는 그런 고급기능이 있지 않다.
빈 공간이 있어도 새로운 레코드 추가 시 맨 마지막 레코드 뒤에 붙게 된다.
그래서 이렇게 중간 레코드가 지워지게 되면 채워지지 못하는 빈 공간들이 생겨 공간의 낭비가 발생한다.
그래서 빈 공간이 생기면 그 공간을 메꾸기 위해 자료를 위로 올리는 작업을 해준다.▼

장점 / 단점
딱 보기만 해도 비효율적인 이 heap을 도대체 왜 사용하는 것일까?
Heap은 단순히 저장만 하는 용도로는 적합하다.
맨 뒤의 레코드에 붙이기 때문에 저장할 때 추가적인 연산이 들어가지 않는다.
조회하는데에 엄청난 시간이 든다는게 단점이지만, 단순히 정보를 저장하는데 집중하는 DB에서는 그 이점을 살리기가 좋다.
단순 저장 후 조회가 잘 이뤄지지 않는 DB에서 heap을 효과적으로 사용할 수 있다.
Hash
Hash는 자료구조에서 많이 봤을 것이고, 자료구조에서 본 그 hash를 말하는게 맞다.
구조 / 삽입 / 조회 / 삭제
Hash는 어떤 값을 hash Function에 적용하여 새롭게 나온 값을 토대로 bucket에 집어넣는 구조를 하고 있다. ▼

삽입, 조회, 삭제 모두 hash Function에 의존하는 형태를 하고 있다.
장점 / 단점
Hash는 hash Function에 전적으로 의존하는 형태지만, hash Function은 단순 사칙 연산을 하는 경우가 많아 굉장히 빠르다.
그렇기에 저장도 빠르고 조회도 빠르다.
조회가 빠르니 당연히 삭제도 빠르다.
그렇다면 hash가 인덱싱의 절대적 우위를 점하고 있는게 아닌가 싶을 수 있는데 hash에는 치명적인 단점이 있다.
아래의 SQL문을 보자. ▼
SELECT name
FROM Students
WHERE grade > 50 AND grade < 80
조건에 맞는 값이 있는지 질의하는 단순한 SQL문이지만 hash는 이 요청을 수행하는데 어려움을 겪는다.
Hash는 특정한 값을 찾는데는 빠르지만, 범위를 구할 때는 모든 값에 대해 연산을 수행해야되기에 굉장히 비효율적으로 구하게 된다.
그 이유는 특정한 값이 hash 함수를 통해 인덱스로 바뀌는데, 바뀐 값이 바뀌고도 순서를 유지한다는 보장이 없기 때문이다.
아래와 같이 정렬된 수들이 있다고 해보자. ▼
$$ 10,\ 20,\ 30,\ 40,\ 50 $$
그리고 hash 함수는 아래와 같다고 해보자. ▼
$$ int\ \ hash(int\ \ x) \{ \ return\ \ x \ \% \ 7 ; \} $$
위의 값을 모두 hash 함수에 넣으면 그 결과는 아래와 같이 나오며 순서가 바뀐다. ▼
$$ 3,\ 6,\ 2,\ 5,\ 1 $$
그렇기에 10과 50을 단순히 hash 함수에 넣는다고 그 범위가 구해지지 않아 bucket의 모든 값을 확인해봐야한다는 단점이 있다.
Sorted File
이름 그대로 정렬하여 저장하는 방식이다.
구조
Sorted file은 heap과는 다르게 들어온 순서가 아니라 데이터의 정렬 순서에 따라 저장된다. ▼
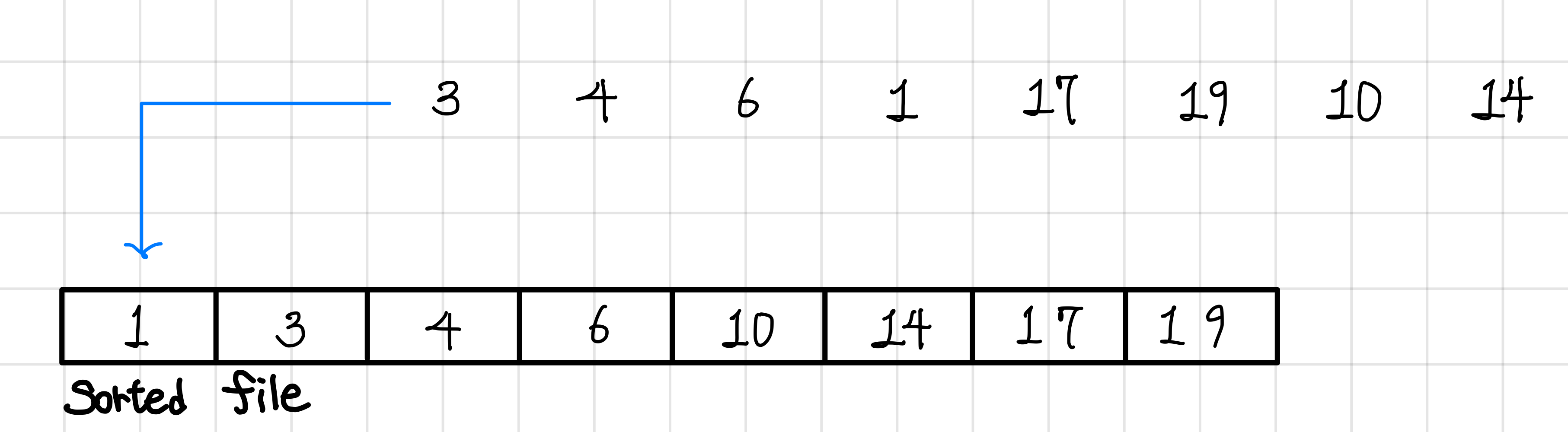
조회
정렬이 되어있다면 이진 탐색을 이용하여 $ log_{2}N $ 의 시간복잡도로 조회가 가능하다.▼

이정도 속도면 hash보다는 느리지만 빠른 편에 속한다.
삽입 / 제거
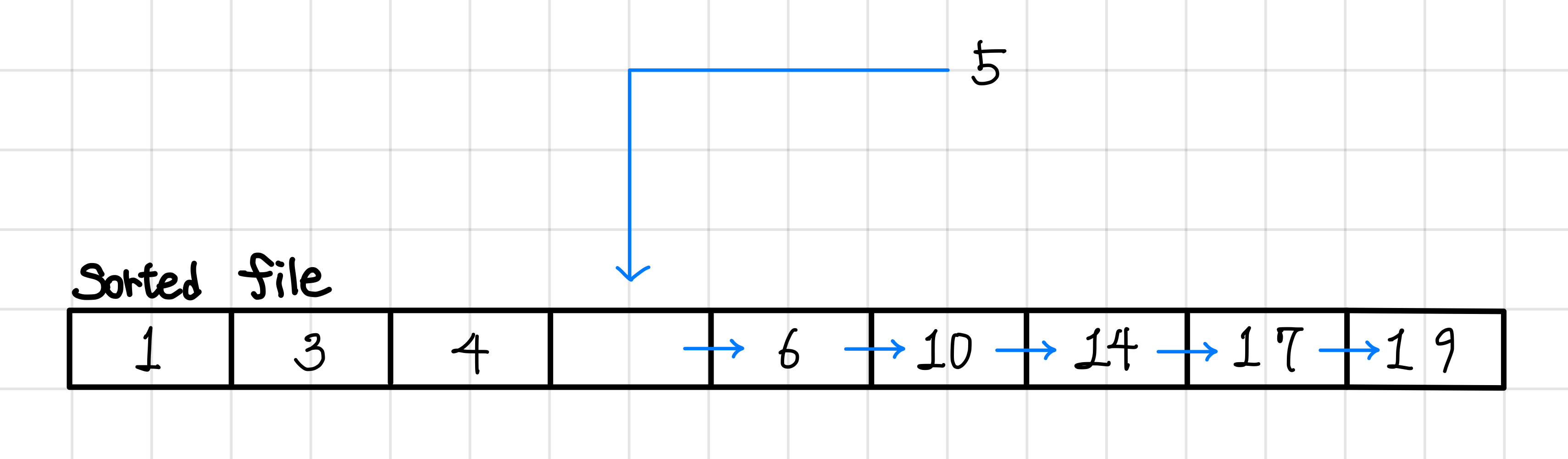
5라는 값을 넣고 싶다고 해보자.
그러면 일단 $log_{2}N$ 의 시간 복잡도로 값을 넣을 위치를 찾는다.▼

값을 넣기 위해 4 뒤의 값을 전부 뒤로 밀어야한다.▼
10을 지운다고 하면 역시 $log_{2}N$의 시간 복잡도로 값을 찾는다.
값을 지우고 나면 값을 전부 당겨야한다.▼

찾을 때는 $log_{2}N$, 넣고 지울 때는 선형 시간으로 밀고 당긴다.
장점 / 단점
Sorted File의 장점은 조회가 빠른 편이라는 것이다.
아무리 빨라봤자 hash보다는 느리긴 하지만 어느정도 균형이 잘 맞춰져있다.
그리고 핵심적인 장점은 해쉬는 하지 못하는 범위 연산을 할 수 있다.
그렇지만 단점은 쓰고, 갱신할 때 오버헤드가 있다.
heap 만큼 빨리 쓸 수는 없다.
가장 좋은 인덱싱 기법은 무엇?
사실 절대적으로 다른 인덱싱 구조를 압도하는 그런 인덱싱 구조는 없다.
다들 일장일단의 성격을 갖고 있고, 다른 모든 점이 안좋아도 특별히 한 부분에서 압도적인 성능을 보여주는 것도 있다.
중요한 것은 Workload다.
DB에 무엇을 주로 요청하는가가 정말 중요하다.
만약 내가 DB에 주로 조회를 요청하면 hash가 유리하다.
그 중에서도 범위 조회가 필요하면 sorted file이 유리하다.
이렇게 상황마다 적절한 인덱싱을 찾는게 중요하다.
그런데 이렇게 해도 뭔가 아쉬울 것이다.
"조회, 삽입, 제거, 수정 모든 부분에서 속도가 나는 인덱싱은 없을까?"
하는 아쉬움이 남을 것이다.
모든 면에서 우월한 인덱싱은 없지만 그런 욕구를 최대한 충족시키기 위해 나온 인덱싱이 있다.
바로 B+ Tree 인덱싱이다.
하지만 이 역시 하이브리드형으로 모든 부분에서 장점을 챙기기 위해 나온 것이므로 상황에 맞춰 적절하게 사용하는 것이 좋다.




