

문제
우현이는 어린 시절, 지구 외의 다른 행성에서도 인류들이 살아갈 수 있는 미래가 오리라 믿었다. 그리고 그가 지구라는 세상에 발을 내려 놓은 지 23년이 지난 지금, 세계 최연소 ASNA 우주 비행사가 되어 새로운 세계에 발을 내려 놓는 영광의 순간을 기다리고 있다.
그가 탑승하게 될 우주선은 Alpha Centauri라는 새로운 인류의 보금자리를 개척하기 위한 대규모 생활 유지 시스템을 탑재하고 있기 때문에, 그 크기와 질량이 엄청난 이유로 최신기술력을 총 동원하여 개발한 공간이동 장치를 탑재하였다. 하지만 이 공간이동 장치는 이동 거리를 급격하게 늘릴 경우 기계에 심각한 결함이 발생하는 단점이 있어서, 이전 작동시기에 k광년을 이동하였을 때는 k-1 , k 혹은 k+1 광년만을 다시 이동할 수 있다. 예를 들어, 이 장치를 처음 작동시킬 경우 -1 , 0 , 1 광년을 이론상 이동할 수 있으나 사실상 음수 혹은 0 거리만큼의 이동은 의미가 없으므로 1 광년을 이동할 수 있으며, 그 다음에는 0 , 1 , 2 광년을 이동할 수 있는 것이다. ( 여기서 다시 2광년을 이동한다면 다음 시기엔 1, 2, 3 광년을 이동할 수 있다. )
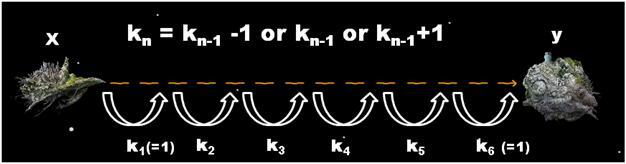
김우현은 공간이동 장치 작동시의 에너지 소모가 크다는 점을 잘 알고 있기 때문에 x지점에서 y지점을 향해 최소한의 작동 횟수로 이동하려 한다. 하지만 y지점에 도착해서도 공간 이동장치의 안전성을 위하여 y지점에 도착하기 바로 직전의 이동거리는 반드시 1광년으로 하려 한다.
김우현을 위해 x지점부터 정확히 y지점으로 이동하는데 필요한 공간 이동 장치 작동 횟수의 최솟값을 구하는 프로그램을 작성하라.
입력
입력의 첫 줄에는 테스트케이스의 개수 T가 주어진다. 각각의 테스트 케이스에 대해 현재 위치 x 와 목표 위치 y 가 정수로 주어지며, x는 항상 y보다 작은 값을 갖는다. (0 ≤ x < y < 2 ^ 31)출력각 테스트 케이스에 대해 x지점으로부터 y지점까지 정확히 도달하는데 필요한 최소한의 공간이동 장치 작동 횟수를 출력한다.
문제 링크
1011번: Fly me to the Alpha Centauri
우현이는 어린 시절, 지구 외의 다른 행성에서도 인류들이 살아갈 수 있는 미래가 오리라 믿었다. 그리고 그가 지구라는 세상에 발을 내려 놓은 지 23년이 지난 지금, 세계 최연소 ASNA 우주 비행
www.acmicpc.net
풀이
이 문제를 직접 이동해가며 계산하기는 굉장히 힘들다.
'하지만 y지점에 도착해서도 공간 이동장치의 안전성을 위하여 y지점에 도착하기 바로 직전의 이동거리는 반드시 1광년으로 하려 한다.'
이 문제 조건 때문인데, 별 거 아닌 것같아 보여도 이 제약 조건 때문에 우리는 항상 최대 속도(광년)로 움직일 수 없게 된다.
속도를 계속 높여서 1, 2, 3, ... 과 같이 움직였다가는 마지막에는 1로 움직이라는 조건을 만족할 수 없다.
속도는 항상 1 차이로만 조절할 수 있기 때문이다.
그래서 우리가 직접 이동해가며 계산하려면 속도를 줄일 지점도 생각하며 움직여야하는데 그게 여간 쉽지 않고, 프로그램에 그 구간이 정확히 어디인지 명시하기도 쉽지 않다.
점화식 구하기
그렇다면 어떻게 접근해야할까?
방금까지 우리는 광년에 초점을 두고 움직였다.
하지만 조건을 다시 생각해보자, 우리가 구하려는건 이동 장치 작동 횟수의 최솟값이다.
이동 장치 작동 횟수에 초점을 둬보자는 것이다.▼

이동 장치 작동 횟수에 따른 최대 이동 방식과 거리는 아래와 같은 패턴을 보인다.
이를 통해 작동 횟수에 따른 최대 이동 거리의 점화식을 얻을 수 있다.
먼저 홀수 번호만 따로 보자.▼

이동 방법이 좌우 대칭 되어 있으며 최대 이동 거리는 제곱수 라는 것을 알 수 있다.▼

짝수 번호 또한 이동 방법이 좌우 대칭 되어 있는데, 최대 이동 거리에는 그렇다 할 특징이 보이지 않는다.
하지만 이동 방법을 잘 보면 최대 이동 거리의 특징을 알아 낼 수 있다.▼

이전 수(홀수)에 맞춰 일정한 수가 더해지는 것을 볼 수 있다.
이 정도 패턴을 구했다면 점화식을 얻을 수 있다.▼

프로그램 동작
이런 점화식을 얻어냈는데, 한 가지 함정이 있다.
우리가 지금 구한 점화식은 우리가 정답으로 제출해야 할 작동 횟수가 변수로 들어간다.
그렇다고 점화식을 구한 게 헛된 일은 아니다.
우리는 점화식을 역으로 사용해서 작동 횟수를 구할 것이다.
거리에 해당하는 수가 들어오면 그 수는 홀수 번호의 이동 거리와 다음 홀수 번호의 이동 거리 사이에 들어올 것이다.
그러면 이런 부등호가 성립하게 된다.
홀수 번호 이동 거리 <= 주어진 거리 < 다음 홀수 번호 이동 거리
그런데 앞에서 봤듯이 홀수 번호는 제곱근이다.
제곱근의 성질 중에는 이런 성질이 있다.
√4 = 2
√5 = 2.xx
...
√9 = 3
특정 제곱수가 되기 전까지는 정수 부분은 가장 작은 제곱수의 제곱근과 같다.
그리고 우리는 실수형을 정수형에 넣으면 소수점이 사라지는 성질도 이용할 것이다.
그러면 주어진 거리의 제곱근은 무조건 홀수 번호 이동 거리의 제곱근과 같아지게 된다.
즉, 이걸로 우리는 홀수 번호를 구할 수 있게 됐다.
홀수 번호를 통해 주어진 거리가 몇번과 몇번 사이에 속하는 지 알 수 있게 되었다.
만약, 주어진 거리가 3번의 최대 거리와 4번의 최대 거리 사이에 속한다면 3번으로는 부족하지만 4번으로는 가능하다는 소리이므로 답은 4가 된다.
예시▼

Swift 코드
import Foundation
let T = Int(readLine()!)!
for i in 0..<T {
let c = readLine()!.split(separator: " ").map { Int(String($0))! }
let x = c[0]
let y = c[1]
var n = Int(Double(y - x).squareRoot()) * 2 - 1
if (y - x) == 1 {
print(1)
} else if (y - x) == (n + 1) / 2 * (n + 1) / 2 {
print(n)
} else if (y - x) > (n + 1) / 2 * (n + 1) / 2 , (y - x) <= ((n + 1) / 2 + 1) * (n + 1) / 2 {
n += 1
print(n)
} else if (y - x) > ((n + 1) / 2 + 1) * (n + 1) / 2 {
n += 2
print(n)
}
}
pow()함수나 squareRoot()함수나 인수를 Double형으로 받고 Double형으로 반환하기 때문에 형변환을 해줘야 한다.
C++ 코드
#include <iostream>
#include <cmath>
using namespace std;
int T;
long long x, y, n;
void input() {
cin >> x >> y;
}
void solution() {
n = (long long)sqrt((double)(y - x)) * 2 - 1;
if ((y - x) == 1) {
cout << 1 << '\n';
} else if ((y - x) == (n + 1) / 2 * (n + 1) / 2) {
cout << n << '\n';
} else if ((y - x) > (n + 1) / 2 * (n + 1) / 2 && (y - x) <= ((n + 1) / 2 + 1) * (n + 1) / 2) {
n += 1;
cout << n << '\n';
} else if ((y - x) > ((n + 1) / 2 + 1) * (n + 1) / 2) {
n += 2;
cout << n << '\n';
}
}
void solve() {
cin >> T;
for (int i = 0; i < T; i++) {
input();
solution();
}
}
int main() {
solve();
}
Swift로 풀었을 때는 맞았는데, Swift로 풀었던 거 그대로 다시 풀었더니 계속 틀려서 이유를 한참 찾았다.
Swift의 Int는 우리가 흔히 알고 있는 32비트의 Int가 아니다.
Swift의 Int는 64비트로 C++의 long long과 같은 크기다.
따라서 Swift에서 Int로 받았지만, 실제 계산은 long long으로 행해진다는 것이다.
무언가 이상하다고 생각되어 중간 계산 비교부분을 출력해보니 음수값이 나와서 오버플로우가 일어나는 것을 알았다.
C++로 PS하면서 오버플로우에 조금 더 조심하게된 거 같다.
'Algorithm > PS' 카테고리의 다른 글
| 백준 1021번 회전하는 큐 - SWIFT (0) | 2024.02.06 |
|---|---|
| 백준 1019번 책 페이지 - SWIFT (0) | 2024.02.06 |
| Swift로 PS 하기 (0) | 2024.01.20 |
| 백준 1092번 배 - SWIFT (0) | 2024.01.20 |
| 백준 16234번 인구 이동 - SWIFT (0) | 2024.01.20 |




