

문제
승택이는 강을 건너려 한다.
승택이는 수영을 못하기 때문에, 강에 놓인 징검다리를 밟고 건너갈 것이다.
승택이는 수영은 못하지만 제자리뛰기는 정말 잘한다. 원하는 어느 곳으로든지 점프해서 바로 갈 수가 있다.
승택이는 이제 강의 한쪽 변 앞에 서 있다.
강엔 1번부터 시작해 2번, 3번, ... , N번 징검다리가 차례대로 놓여 있다.
강의 폭이 넓은 탓에 징검다리의 수는 엄청나게 많다.
이 징검다리를 모두 밟고 싶지는 않았던 승택이는 제자리뛰기 실력을 발휘해 적절한 개수의 징검다리만을 밟고 가기로 했다.
물론 강 건너편으로 바로 점프하는 것도 가능하지만, 더 재미있게 강을 건너기 위해 승택이는 다음과 같은 규칙을 정했다.
- 첫 징검다리는 점프해서 아무 것이나 밟을 수 있다. 이 점프가 첫 점프이다.
- 두 번째 점프부터는 이전에 점프한 거리보다 1 이상 더 긴 거리를 뛰어야만 한다.
- N번 징검다리는 반드시 밟아야 한다.
- N번 징검다리를 밟은 후 강 건너로 이동할 땐 점프를 하지 않으므로 위의 규칙이 적용되지 않는다.
승택이가 위의 규칙을 지키며 강을 건널 때, 밟을 수 있는 징검다리의 최대 수는 몇 개일까?
입력
첫째 줄에 테스트 케이스의 수 T가 주어진다.
각 테스트 케이스는 정수 한 개로 이루어져 있으며, 징검다리의 총 수 N을 의미한다. (1 ≤ N ≤ 10^16)
출력
각 테스트 케이스마다 한 줄에 승택이가 밟을 수 있는 최대 징검다리 수를 출력한다.
문제 링크
https://www.acmicpc.net/problem/11561
풀이
접근
규칙을 간단하게 요약하자면 N개의 징검다리가 있고, 이전에 a개 건넜다면 그 다음엔 최소 a+1개를 건너야 한다는 규칙이 된다. ▼

그 와중에 우리가 구하고자 하는 것은 최대로 밟는 징검다리의 수다. 그렇기에 징검다리를 건널 때 항상 최소치로 움직여야 하고, 가장 작은 움직임은 1이기에 우리는 1부터 시작하여 하나씩만 증가하여 움직인다. ▼
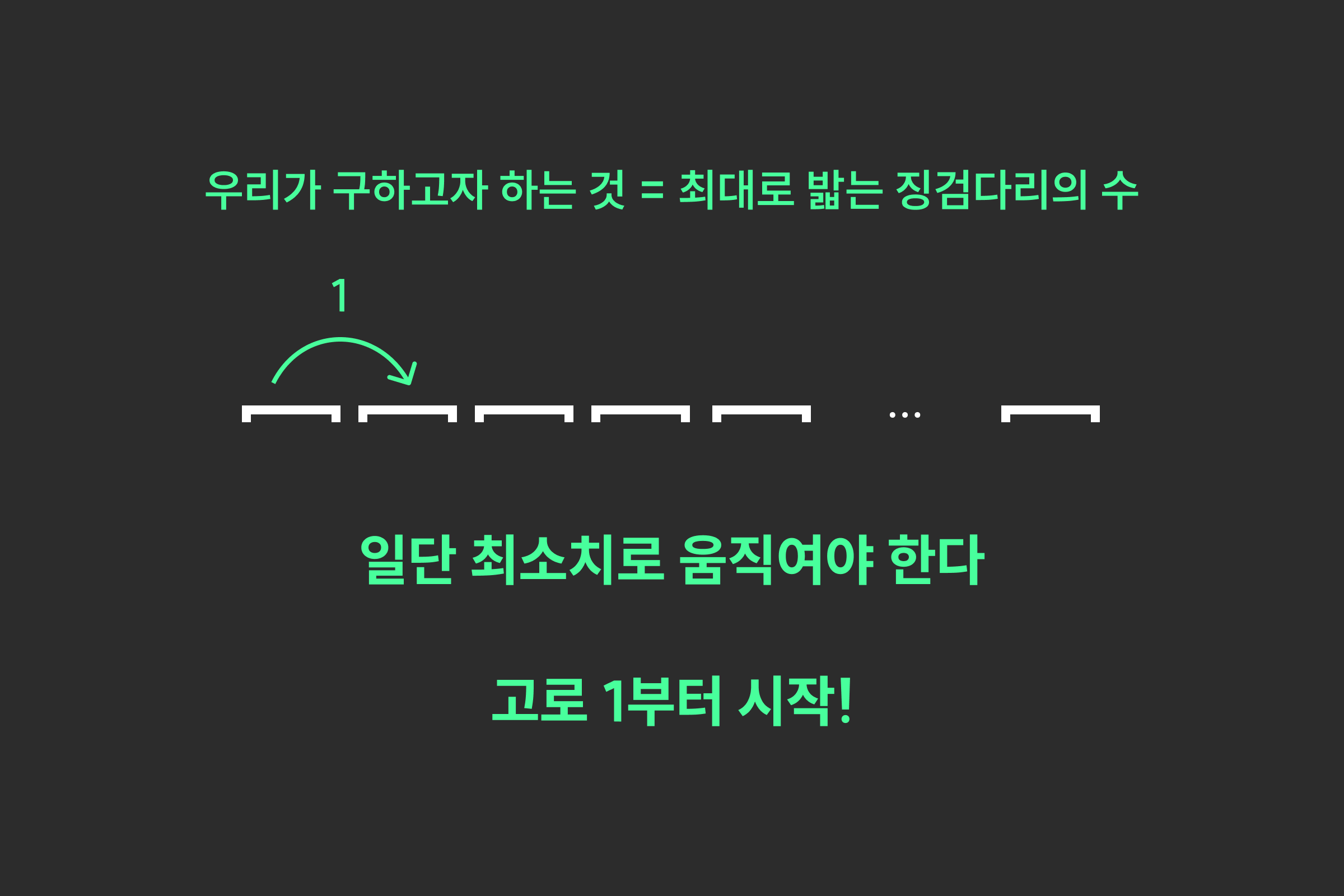
그런데 그렇게 움직이다 보면 마지막 돌을 밟아야 한다는 규칙에 다다른다.
N은 58이고, 1부터 10까지 움직인 상황이라고 해보자. 이러면 우리가 움직인 거리는 총 55, 남은 거리는 3이다.
하지만 다음에 움직여야하는 거리는 11이므로 마지막 징검다리에 도달할 수 없다. ▼
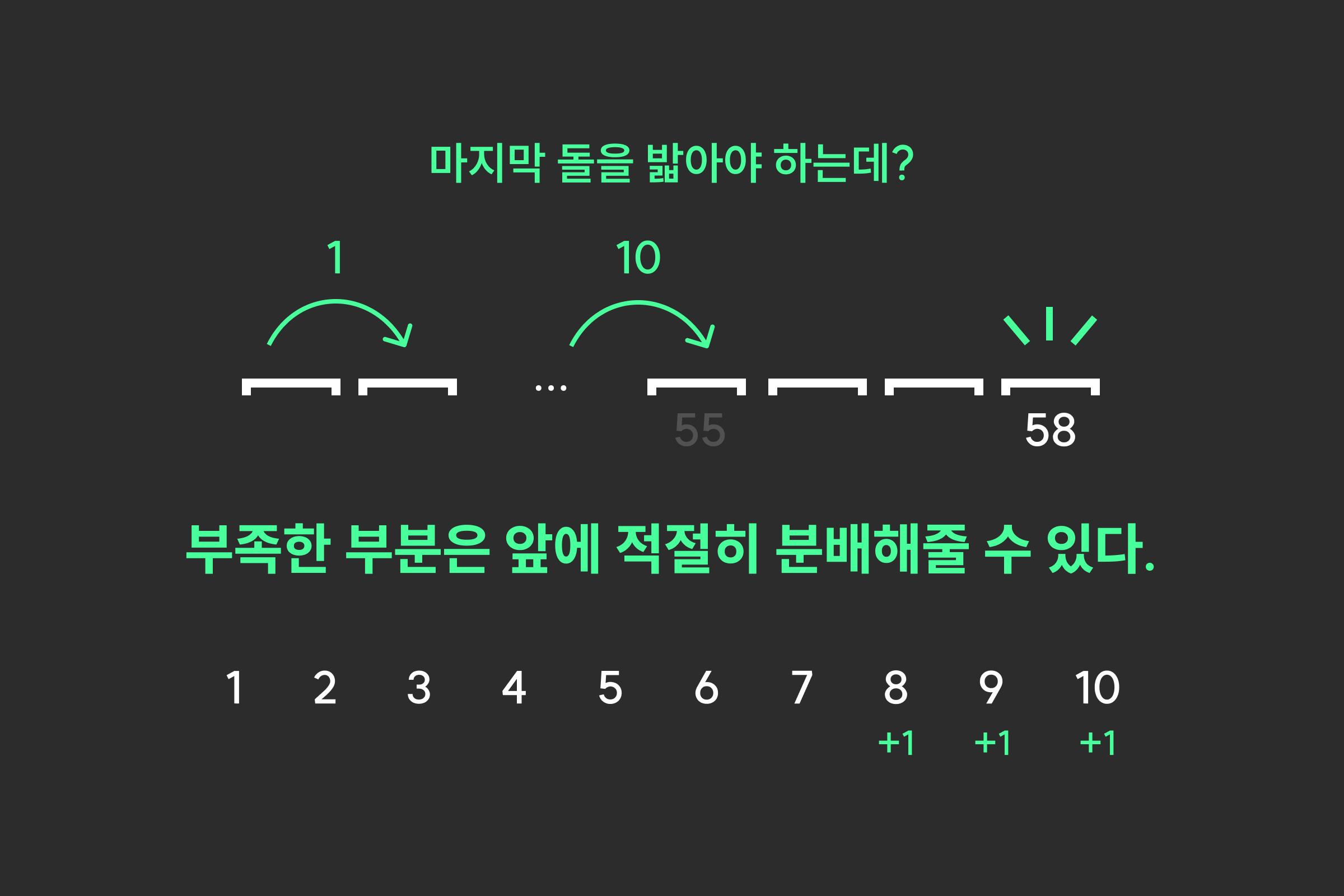
하지만 그건 별로 상관없다. 우리는 무조건 이전 움직임보다 1크게 움직이는게 아니라, 최소 1크게 움직이는 것이기에 앞의 움직임들에 적절히 분배해주면 된다.
그러면 최종적으로 1, 2, 3, 4, 5, 6, 7, 9, 10, 11을 움직여 58을 맞출 수 있다.
'와 그러면 이제 급수 공식 써서 풀어야지!'
'그냥 앞에서부터 하나씩 늘려가면 되겠네!'
이러면 무조건 시간초과다. 만약에 N이 최대값인 10의 16승으로 들어오게 되면, 억대의 연산을 해야하기에 제한시간을 훌쩍 넘어버린다. ▼

그렇기에 우리는 이분탐색을 사용해야한다.
이분탐색
최대값을 N으로 두고, 양 극단의 중앙의 값으로 급수 계산을 하며 범위를 좁혀나가면 된다. ▼

이렇게 하면 시간내에 정답을 구할 수 있다!
C++ 코드
#include <iostream>
using namespace std;
long long T, N;
void binarySearch() {
unsigned long long left = 1;
unsigned long long right = N;
unsigned long long mid;
while (left <= right) {
mid = (left + right) / 2;
if (mid * (mid + 1) / 2 <= N) {
left = mid + 1;
} else {
right = mid - 1;
}
}
cout << right << '\n';
}
void solve() {
cin >> T;
while (T--) {
cin >> N;
binarySearch();
}
}
int main() {
solve();
}
문제를 풀 때 한 가지 주의해야할 점이 있는데, 바로 변수의 값의 범위다.
10의 16승이라는 값만 봤을 때는 `long long`으로 충분히 커버가 가능하다고 생각했는데, 급수 계산을 할 때 값을 초과할 수 있다.
그렇기에 `unsigned long long`으로 범위를 2배 늘려줘야 커버가 가능해진다.
'Algorithm > PS' 카테고리의 다른 글
| 백준 24479번 알고리즘 수업 - 깊이 우선 탐색1 - C++, SWIFT (1) | 2024.10.31 |
|---|---|
| 프로그래머스 입국심사 - C++ (0) | 2024.10.30 |
| 백준 1072번 게임 - C++ (2) | 2024.10.28 |
| 백준 2467번 용액 - SWIFT (0) | 2024.08.04 |
| 백준 2467번 용액 - SWIFT (0) | 2024.06.12 |




