

문제
프렉탈 평면은 다음과 같이 커진다. 시간 0에서 프렉탈은 흰색 정사각형 하나이다. 단위 시간(1)이 진행될 때마다 N×N개의 크기가 동일한 단위 정사각형으로 나누어진다. 만약 나누어진 정사각형이 흰색이라면 가운데 K×K 정사각형이 검정색으로 채워진다. N과 K는 둘 다 홀수이거나, 둘 다 짝수이다.
예를 들어, N=3, K=1이라면, 시간 1에 3×3 정사각형이 된다. 가운데 정사각형은 검정색이고, 나머지는 흰색이 된다. 시간 2때 9×9 정사각형이 되고, 17개는 검정이고, 나머지는 흰색이다.

s, N, K, R1, R2, C1, C2가 주어질 때, 시간 s일 때, R1행 C1열부터 R2행 C2열까지의 모습을 출력하는 프로그램을 작성하시오.
입력
첫째 줄에 7개의 정수 s, N, K, R1, R2, C1, C2가 주어진다.
출력
첫째 줄에 문제의 정답을 출력한다. 첫째 줄에 R1행의 모습을 출력하고 이런 식으로 총 R2-R1+1개의 줄에 출력하면 된다. 각 행의 모습을 출력할 때, C1열부터 C2열까지 차례대로 흰색이면 숫자 '0' 검정이면 숫자 '1'을 출력한다. 숫자 사이에 공백을 넣으면 안 된다.
제한
- 0 ≤ s ≤ 10
- 3 ≤ N ≤ 8
- 1 ≤ K ≤ N - 2
- (N - K) mod 2 = 0
- 0 ≤ R1, R2, C1, C2 ≤ N^s - 1
- R1 ≤ R2 ≤ R1 + 49
- C1 ≤ C2 ≤ C1 +49
풀이
문제와 그림을 보고서 순간 여러 생각이 스쳐 지나갔다.
‘이걸 배열에 담아서 그린 다음에, 범위 대로 출력하면 쉽겠다.’
‘근데 메모리 제한에 걸릴 거 같은데… 최대 범위로 들어와도 메모리에는 안걸리겠다.’
‘다시 생각해보니까 이거 다 그리는데 연산이 억이 넘어갈 거 같은데, 역시 너무 쉽게 생각했나?’
위의 생각이 스쳐지나가고 조금 더 고민해보니 문제에서 제시한 프랙탈을 그릴 필요가 없다는 것을 깨달았다.
접근법
모든 프랙탈을 그리지 않고 제시된 범위의 그림을 어떻게 그릴까?
그것은 프랙탈의 규칙을 이용하면 된다.
이 문제에서 제시한 프랙탈은 가장 자리는 흰색, 가운데는 검정색이라는 기본 구조가 있다.
프랙탈의 특징으로 인해 우리는 기본 구조를 토대로 대략적인 모양을 알 수 있다.
예를 들어서 위에 제시된 대로 N이 3, K가 1이면 3의 제곱수 크기 마다 규칙이 나타난다.▼
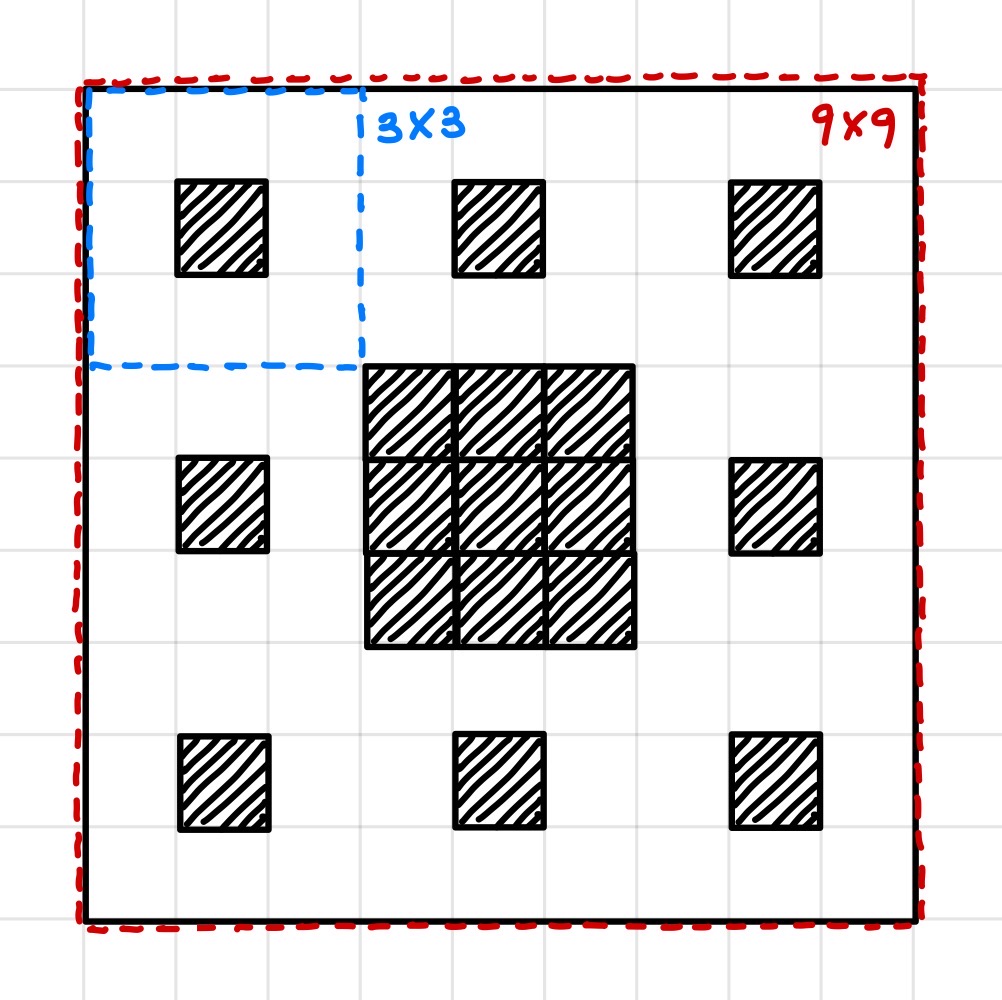
다들 잘 알겠지만, 위의 프랙탈 구조는 만약에 한 변의 크기가 $n^m$이라면, 이는 한 변의 크기가 $n^{m-1}$인 프랙탈 구조가 모여서 생성이 된다.
위의 그림처럼 9 * 9 크기 프랙탈은 3 * 3 크기 프랙탈 8개와 가운데 검정 블럭이 모여서 만들어진다.
즉, 아래와 같은 형태다.▼

이런 특징들을 통해 우리는 특정 좌표가 주어지면, 수학적으로 해당 좌표가 프랙탈의 어느 부분에 속해있는 지 알 수 있다.
프로그램 동작
예를 하나 보면서 확인해보자.
위의 그림과 같은 N이 3이고, K가 1, s가 2인 프랙탈이 있다고 하자.
여기서 (4, 1) 좌표의 색상을 알아내보자.▼

첫번째로는 해당 좌표가 가운데에 있는지 확인해보자.
검정 블럭 좌표는
$ 단위\ 프랙탈\ 크기(N^{m-1})\ *\ (N -K)\ /\ 2 $
부터
$ 단위\ 프랙탈\ 크기(N^{m-1})\ *\ (N+K)\ /\ 2 $
이다.
예시 좌표가 0부터 시작하지 않아서 약간은 차이가 있지만, (4, 1)는 가운데 검정 블럭에 있지 않다.
그렇다면 (5, 2)라는 좌표는 필연적으로 테두리의 프랙탈에 있다는 것이다.▼

그러면 해당 좌표에 있는 프랙탈로 이동해서 보면 될 거 같은데, 좌표를 특정하는게 약간 복잡해진다.
내가 색을 찾고자 하는 좌표의 프랙탈을 특정하고, 해당 좌표에서 계산을 다시 하게 되면 추가적인 연산이 계속해서 필요해진다.
하지만 프랙탈의 특징을 이용하면 간단하게 해결이 가능해진다.
잠깐 해당 좌표는 다른데 넣어두고, 아래의 두 좌표를 보자.▼

두 좌표는 꽤나 멀리 떨어져 있고, 아무런 관련도 없어보인다.
하지만 각 좌표가 해당한 프랙탈로 한정지어보면 둘은 동일한 위치에 있다.▼

그래서 우리는 찾고자 하는 좌표로 직접 이동하는게 아니라, 해당 좌표가 상대적으로 어디에 위치해 있는지로 판별할 것이다.
그러면 우리가 찾고자 했던 좌표인 (4, 1)는 이 좌표가 해당한 프랙탈 크기로 나누어 나머지를 구하면 상대 좌표가 나온다.▼
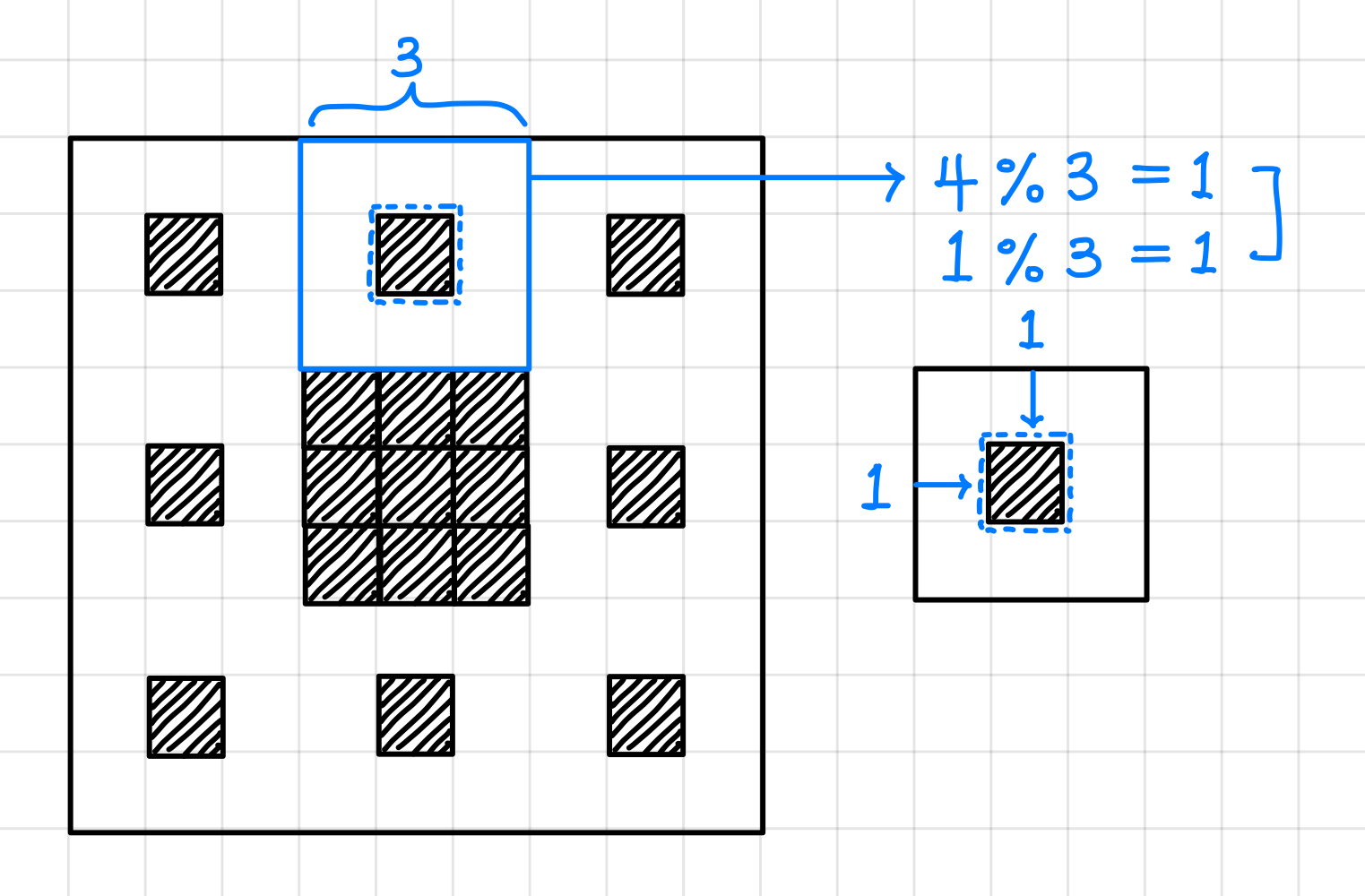
그러면 더 이상 해당 좌표로 볼 필요가 없이 위에서 구한 상대적이 좌표로 보면 된다.
위에서 구한 상대 좌표로 아까 했던 검정 블럭 부분을 확인해본다.▼

검정 블럭 부분에 해당 좌표가 속해 있으므로 좌표 (4, 1)는 검정색이다.
이제 지금까지 했던 과정을 우리가 구하고자 하는 모든 좌표에 수행해주면 된다.
프랙탈 크기가 1까지 줄어들었는데 검정 블럭에 속하지 않았다면, 이는 흰색이라는 의미이다.
C++ 코드
#include <iostream>
using namespace std;
int s, N, K, R1, R2, C1, C2;
void input() {
cin >> s >> N >> K >> R1 >> R2 >> C1 >> C2;
}
int solution(int len, int x, int y) {
int border;
if (len == 1)
return 0;
border = len / N;
if (x >= border * (N - K) / 2 && x < border * (N + K) / 2
&& y >= border * (N - K) / 2 && y < border * (N + K) / 2) {
return 1;
}
return solution(border, x % border, y % border);
}
void solve() {
int len = 1;
input();
while (s--) {
len *= N;
}
for (int i = R1; i <= R2; ++i) {
for (int j = C1; j <= C2; ++j) {
cout << solution(len, i, j);
}
cout << '\n';
}
}
int main() {
solve();
}'Algorithm > PS' 카테고리의 다른 글
| 백준 1181번 단어 정렬 - SWIFT (1) | 2024.02.25 |
|---|---|
| 백준 1167번 트리의 지름 - SWIFT (0) | 2024.02.20 |
| 백준 1065번 한수 - SWIFT, C++ (0) | 2024.02.18 |
| LeetCode 2. Add Two Numbers - C++ (0) | 2024.02.13 |
| LeetCode 1. Two Sum - C++ (0) | 2024.02.13 |




